Completing BlueRaja's answer to answer Ixion' question. Copy-pasting the illustration from said answer here for ease of reading.

Note that :
- it is for grids with no diagnoal movement, but it can be adapted to grids with diagonals and even gridless setups.
- I'm not presenting the most optimized version (which I'm not aware of), more like the idea behind the algorithm
- To not spend too much time writing, I'm not adding schema, but feel free to ask me to add some.
"How is the grid divided into chunks ?"
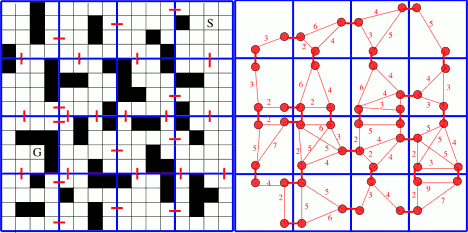
Step 1 : define chunks
Choose an arbitrary chunk size. In BlueRaja's example it is 4. Maybe there are some theoretical way to find the optimal one, but I don't know of them. However finding a good size for speed can be done experimentally once it is implemented in you game. We store chunks in a grid as well.
Note : To know which chunk a cell belongs to, we can simply integer-divide the coordinated of the cell by the size of the chunk. With a chunk of size 4, the (15, 6) cell belongs to the chunk (3, 1).
Step 2 : find gates
For each pair of adjacent chunk A and B, find a pair of cells C_a and C_b so that :
Both A and B are adjacent and open (no obstacle on them), C_a belongs to A, and C_b belongs to B. The pair is a "gate". They are illustrated by red lines on BlueRaja's answer.
You can eventually find all gates for each pair of chunks, it will reduce speed but increase accuracy of pathfinding. You can also do an-in between, for example keeping only gates that have a longer path to each other with obstacles than without obstacles.
Step 3 : build the abstraction graph
Now to build the red graph on the right of the pic.
create an empty graph G.
For each chunk for each inner pair of gate cells (A1, A2) belonging to the chunk cells, compute the best path P_ab between A and B. Then add A1 and A2 to the graph as vertices (if not already in it), and a edge of length P_ab between them. For the vertices, retain the position of the corresponding cell in the initial grid (not chunks).
Additionally, you need a collection associating each chunk'id (position in grid) with its gate vertices, and we need to keep each P_ab in memory for later use.
In the pic, we can see that top-left chunk has two gates, and that the path to link them is of length 3.
We also add edges of length 1 linking adjacent cell gates together, to pass from one chunk to another.
optional : do more abstractions recursively.
"how is the heuristic evaluated for the hierarchy / how to pathfind with it?"
We have our graph, now, now let's do some pathfinding.
We want to go from cell S (start) to E (end).
Step 1 : Link S to its chunk gates
Knowing the coordinates of the cell S stands, we can know which chunk it stands in. We access the chunk, and then, on subset of the grid that belongs to the chunk, we compute all best-path (or heuristic-best path) P_sa from S to each cell gate A of the chunk. We add S to G as a vertice, and also edges for each P_sa computed. We keep those paths in memory.
Step 2 : same, but for E
Step 3 : run pathfinding or on G
Now we use a pathfinding algorithm to compute best path from S to E on graph G. We then use stored grid-paths to recompute the full path. Eventually, we don't need full path but just enough of the first steps of the path so that the entity we drive can move until the next pathfinding triggering.
Step 4 : clearing
Finally, we remove vertices S, E and their attached edges from G, so we can use G to pathfind another entity or another position.
optional : recursive hierarchiy
In case we have more than one level of abstraction, we use level n to find best paths to level n+1 gates in the chunk of level n+1, recursively.