First of all, in the case of axis-aligned rectangles, Kevin Reid's answer is the best and the algorithm is the fastest. Now, to a more general answer:
#How to tell in the general case whether two convex shapes intersect?#
I'll give you an algorithm that works for all convex shapes and not just hexagons.
Suppose X and Y are two convex shapes. They intersect if and only if they have a point in common, i.e. there is a point x ∈ X and a point y ∈ Y such that x = y. If you regard the space as a vector space, then this amounts to saying x - y = 0. And now we get to this Minkowski business:
The Minkowski sum of X and Y is the set of all x + y for x ∈ X and y ∈ Y. Supposing (-Y) is the set of all -y for y ∈ Y, then given the previous paragraph, X and Y intersect if and only if X + (-Y) contains 0, that is, the origin.
Side remark: why do I write X + (-Y) instead of X - Y ? Well, because in mathematics, there is an operation called the Minkowski difference of A and B which is sometimes written X - Y yet has nothing to do with the set of all x - y for x ∈ X and y ∈ Y (the real Minkowski difference is a little more complex).
So we'd like to compute the Minkowski sum of X and -Y and to find whether it contains the origin. The origin is not special compared to any other point, so that to find whether the origin is within a certain domain, we use an algorithm that could tell us whether any given point belongs to that domain.
The Minkowski sum of X and Y has a cool property, which is that if X and Y are convex, then X+Y is too. And finding whether a point belongs to a convex set is much easier than if that set were not (known to be) convex.
We can't possibly compute all of the x - y for x ∈ X and y ∈ Y because there are an infinity of such points x and y, so hopefully, since X, Y and X + Y are convex, we can just use the "outermost" points defining the shapes X and Y, which are their vertices, and we'll get the outermost points of X + Y, and also some more.
These additional points are "surrounded" by the outermost ones of X + Y so that they do not contribute to defining the newly obtained convex shape. We say that they don't define the "convex hull" of the set of points. So what we do is that we get rid of them in preparation for the final algorithm that tells us whether the origin is within the convex hull.
We therefore get ##A first, naive algorithm## boolean intersect(Shape X, Shape Y) {
SetOfVertices minkowski = new SetOfVertices(); for (Vertice x in X) { for (Vertice y in Y) { minkowski.addVertice(x-y); } } return contains(convexHull(minkowski), Vector2D(0,0)); } The loops obviously have complexity O(mn) where m and n are the number of vertices of each shape. The minkoswki set contains mn elements at most. The convexHull algorithm has a complexity that depends on the algorithm you used, and you can aim for O(k log(k)) where k is the size of the set of points, so in our case we get O(mn log(mn)). The contains algorithm has a complexity that is linear with the number of edges (in 2D) or faces (in 3D) of the convex hull, so it really depends on your starting shapes, but it won't be greater than O(mn).
I'll let you google for the contains algorithm for convex shapes, it's a pretty common one. I may put it here if I have the time.
#But it's collision detection we're doing, so we can optimize that a lot#
We origiannly had two bodies A and B moving without rotation during a timestep dt (from what I can tell by looking at your pictures). Let's call vA and vB the respective speeds of A and B, which are constant during our timestep of duration dt. We get the following:
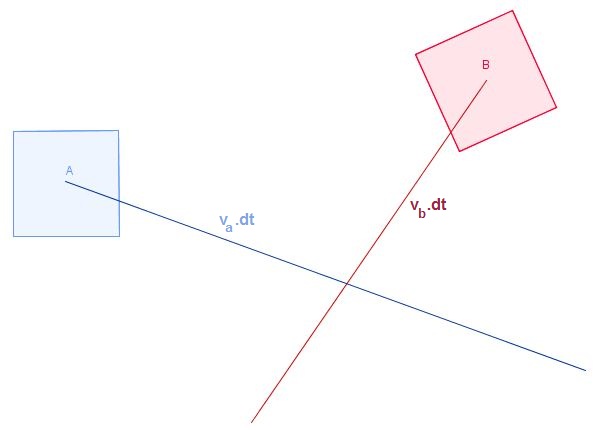
and, as you point out in your pictures, these bodies do sweep through areas (or volumes, in 3D) as they move:

and they end up as A' and B' after the timestep.
To apply our naive algorithm here, we would only have to compute the swept volumes. But we're not doing this.
In reference frame of B, B doesn't move (duh!). And A has a certain velocity with respect to B that you get by computing vA - vB (you can do the converse, compute the relative velocity of B in the reference frame of A).
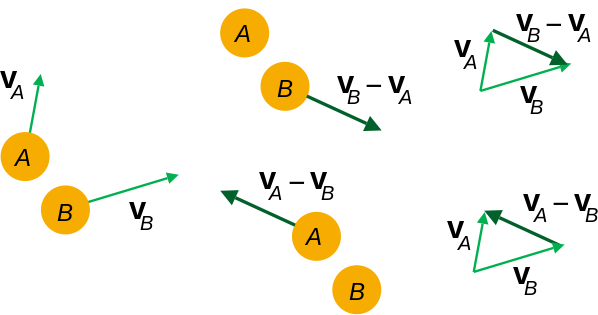
From left to right: velocities in the base reference frame; relative velocities; computing relative velocities.
By regarding B as immobile in its own reference frame, you only have to compute the volume A sweeps through as it moves during dt with its relative velocity vA - vB.
This decreases the number of vertices to be used in the Minkowski sum computation (sometimes greatly).
Another possible optimization is at the point where you compute the volume swept by one of the bodies, let's say A. You don't have to translate all of the vertices making up A. Only those that belong to edges (faces in 3D) whose outer normal "face" the direction of the sweeping. Surely you had noticed that already when you computed your swept areas for the squares. You can tell whether a normal is towards the sweeping direction using its dot product with the sweeping direction, which has to be positive.
The last optimization, that has nothing to do with your question regarding intersections, is really useful in our case. It uses those relative velocities we mentioned and the so-called separating axis method. Surely you know about it already.
Suppose you know the radii of A and B with respect to their centers of mass (that is to say, the distance between the center of mass and the vertex farthest from it), like this:

You only have to even do all this if it is possible that the bounding circle of A meet that of B. We see here that it won't, and the way to tell the computer that is to compute the distance from CB to I as in the following picture and make sure it's smaller than the sum of the radii of A and B:
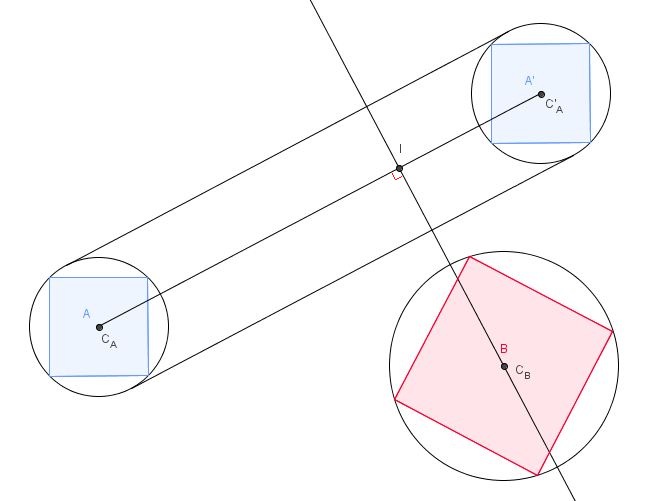
This doesn't work very well with shapes that are rather long, but in the case of squares, it's a perfect heuristic.
To apply this method more generally, you must find the vertex in A that is farthest from the (CA, C'A) line on B's side of it (i.e. which maximizes a dot product, let's call the maximum dA), find the vertex in B that is the furthest towards that line (by maximizing a dot product again, let's call the maximum dB) a make sure that dA + dB < ICB.
That's the equivalent of separating B and the swept volume of A with an axis, meaning they won't collide, but that's much more computationally intensive than the radii method (linear time against a small, constant time).
Our new, better algorithm
boolean mayCollide(Body A, Body B) { Vector2D relativeVelocity = A.velocity - B.velocity; if (separatingAxis(A, B, relativeVelocity)) { return false; // there is a separating axis between them } Volume sweptA = sweptVolume(A, relativeVelocity); return contains(minkowskiMinus(sweptA, B), Vector2D(0,0)); } boolean separatingAxis(A, B, relativeVelocity)) { // whatever method you prefer, see google for the code } SetOfVertices minkowskiMinus(Body X, Body Y) { SetOfVertices result = new SetOfVertices(); for (Vertice x in X) { for (Vertice y in Y) { result.addVertice(x-y); } } return result; } 