How can we find sizes in a uniform tiling of the hyperbolic plane?

Given a certain uniform tiling of the hyperbolic plane (for example, one given by its vertex configuration, if that specifies a tiling unambiguously, or a tiling specified by some other means, whatever that means is?), how can we find

1. The length of a side in the tiling, and
2. The distance from the center of a polygon to the middle of the side of the same polygon, for each polygon type?

For simplicity, we can assume the curvature $\kappa$ of the plane to be $-1$ (or equivalently, the radius $R$, which is defined as $R = \sqrt{-\kappa}$ by some sources, to be $1$).

Note that the the number of sides of each tile and the valence of each vertex is given by the vertex configuration, and that all sides in a uniform tiling have the same length.

I have made the following attempt to calculate 2. for the special case of the tiling $\{p,q\}$ (in the picture I have chosen $p=4$ and $q=6$):

As can be seen, I have used the Poincaré disk model to project the hyperbolic plane to the Euclidean plane, and I have chosen the tile to be centered in the center of the disk. From this figure we can extract a set of equations:

1. $\displaystyle 2q\alpha = 2\pi$ (since the Poincaré disk model is conformal, all $q$ polygons that meet in a corner contributes with the angle $2\alpha$),
2. $\displaystyle 2p\beta = 2\pi$,
3. $\displaystyle \beta + \alpha + \beta' + \frac{\pi}{2} = \pi$ (the corners of the small right triangle has angles $\beta$, $\alpha + \beta'$ and $\pi/2$, respectively),
4. $\displaystyle R = R'\tan\gamma$ (given by the large right triangle which has corners in the circle centers and in the top intersection point between the two circles),
5. $d + R' = R\sin\gamma + R'\cos\gamma$ (the distance between the centers of the circles formed in two different ways),
6. $\displaystyle d^+ - d = R'(1 - \cos\beta')$, and
7. $\displaystyle d^+\tan\beta = R'\sin\beta'$.

From 1., 2. and 3. we get

• $\displaystyle \alpha = \frac{\pi}{q}$,
• $\displaystyle \beta = \frac{\pi}{p}$, and
• $\displaystyle \beta' = \frac{\pi}{2} - \beta + \alpha = \left(\frac{1}{2} - \frac{1}{p} - \frac{1}{q}\right)\pi$.

From 4. we get

• $\displaystyle R' = \frac{R}{\tan\gamma}$,

and combining this with 5. gives $\displaystyle d + \frac{R}{\tan\gamma} = R\sin\gamma + \frac{R}{\tan\gamma}\cos\gamma$, which can be reworked into

• $\displaystyle d = \frac{1 - \cos\gamma}{\sin\gamma}R$.

Now, 6. gives us $\displaystyle d^+ = \frac{1 - \cos\gamma}{\sin\gamma}R + \frac{R}{\tan\gamma}(1 - \cos\beta')$, which can be worked into

• $\displaystyle d^+ = \frac{1 - \cos\gamma\cos\beta'}{\sin\gamma}R$

and 7. gives us $\displaystyle \frac{1 - \cos\gamma\cos\beta'}{\sin\gamma}R\tan\beta = \frac{R}{\tan\gamma}\sin\beta'$, which is equivalent to

• $\displaystyle \cos\gamma = \frac{\sin\beta}{\cos\alpha} $

or

• $\displaystyle \sin\gamma = \frac{\sqrt{\cos^2\alpha-\sin^2\beta}}{\cos\alpha} $

or

• $\displaystyle \tan\gamma = \sqrt{\frac{\cos^2\alpha}{\sin^2\beta} - 1} $

The hyperbolic distance between two adjacent corners of the tile can then be calculate as follows according to this formula I found on Wikipedia, where $P$ and $Q$ are the points in the Poincaré disc of the corners, and $A$ and $B$ are the ideal points at which the unique hyperbolic line that connects $P$ and $Q$ intersects the boundary:

$$ d(p,q)= \ln \frac{ \left| AQ \right| \, \left| PB \right| }{ \left| AP \right| \, \left| QB \right| } $$

I have tried this formula numerically—I constructed $a$ and $b$ numerically, too, by using gyrovector operations—but what I find more practical is to calculate the vector difference $\vec{x} = \ominus P \oplus Q$, and calculate the hyperbolic length of the resulting gyrovector as

$$ \|\vec{x}\|_{\kappa} = 2 \arctan_{\kappa}\left(\|\vec{x}\|_{\text{Euclidean}}\right) $$

where $\vec{x}$ is the Euclidean carrier vector of the hyperbolic point in the Poincaré disk, $\kappa$ is the curvature of the hyperbolic space, and $\arctan_{\kappa}(x)$ is defined as

$$ \arctan_{\kappa}(x) = \begin{cases} \displaystyle \frac{1}{\sqrt{-\kappa}}\tanh(\sqrt{-\kappa} x), & \kappa < 0, \\ \displaystyle x, & \kappa = 0, \\ \displaystyle \frac{1}{\sqrt{\kappa}}\tan(\sqrt{\kappa} x), & \kappa > 0, \end{cases} $$

which follows by the conformal factor of the point in the Poincaré disk (the same type of gyrovectors can also be used for spherical geometry and in Euclidean space). Using these gyrovectors I am also able to correctly position tiles in an arbitrary hyperbolic {p,q} tessellation of the hyperbolic plane in the Poincaré disk, for example this {4,6} tessellation; here is a screenshot from a small demo application I wrote in Python:

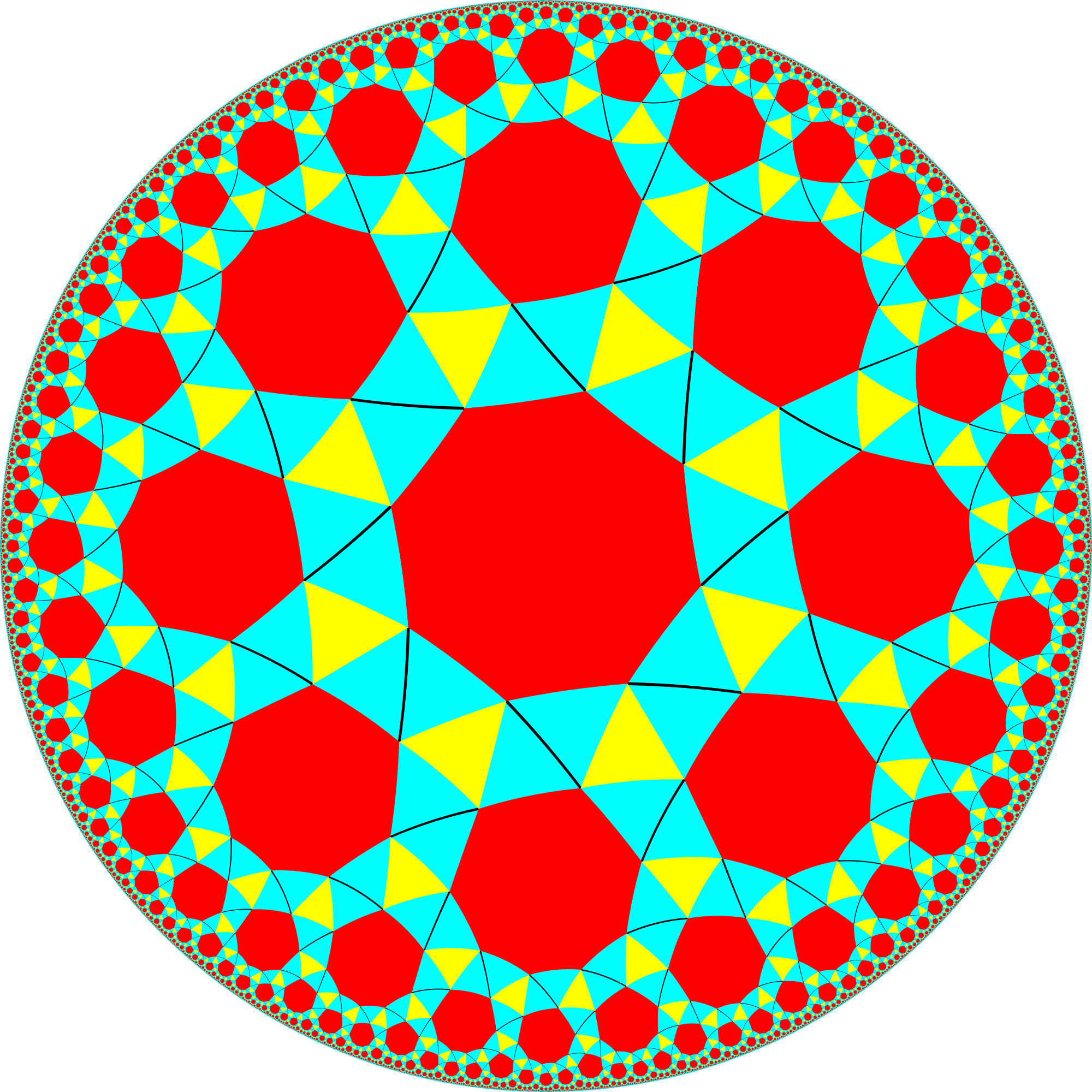
I feel like this is a good start, but it took me quite some time just to be able to calculate what I need in order to work with tiles in this simple case, and I feel like it would be nice if there was some simpler method to do this. Besides, there are many more tilings, for example an endless amount of uniform tilings that consist of more than one tile type and cannot be represented on the form {p,q}, and are therefore more complex. For example this snub tiling, which consists of two different types of tiles:

So, is there some simpler method to calculate the length of a side in a tiling, and the distance from the center of a polygon to the middle of the side of the same polygon, than the method I have used here? Is there some systematic method to do this in the general case for any uniform tiling?