47
$\begingroup$

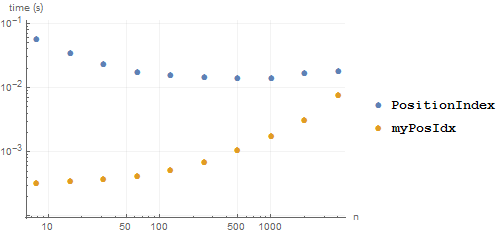
This issue has largely been mitigated in 10.0.1. New timings for the final test below are:

Needs["GeneralUtilities`"] a = RandomInteger[9, 5*^5]; myPosIdx[a] // AccurateTiming cleanPosIdx[a] // AccurateTiming (* see self-answer below *) PositionIndex[a] // AccurateTiming 
0.0149384 0.0149554 0.0545865

Still several times slower here than the readily available alternatives but no longer devastating.

Disconcertingly I have discovered that the new (v10) PositionIndex is horribly slow.

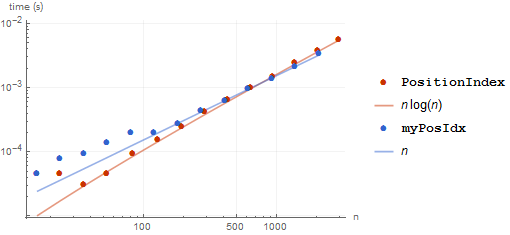
Using Szabolcs's clever GatherBy inversion we can implement our own function for comparison:

myPosIdx[x_] := <|Thread[x[[ #[[All, 1]] ]] -> #]|> & @ GatherBy[Range @ Length @ x, x[[#]] &]

Check that its output matches:

RandomChoice[{"a", "b", "c"}, 50]; myPosIdx[%] === PositionIndex[%] 
True

Check performance in version 10.0.0 under Windows:

a = RandomInteger[99999, 5*^5]; myPosIdx[a] // Timing // First PositionIndex[a] // Timing // First 
0.140401 0.920406

Not a good start for the System` function, is it? It gets worse:

a = RandomInteger[999, 5*^5]; myPosIdx[a] // Timing // First PositionIndex[a] // Timing // First 
0.031200 2.230814

With fewer unique elements PositionIndex actually gets slower! Does the trend continue?

a = RandomInteger[99, 5*^5]; myPosIdx[a] // Timing // First PositionIndex[a] // Timing // First 
0.015600 15.958902

Somewhere someone should be doing a face-palm right about now. Just how bad does it get?

a = RandomInteger[9, 5*^5]; myPosIdx[a] // Timing // First PositionIndex[a] // Timing // First 
0.015600 157.295808

Ouch. This has to be a new record for poor computational complexity in a System function. :o

Improve this question
$\endgroup$
26
  • 10
    $\begingroup$ I like to see this in a Wolfram Blog post and I already hear the first paragraph: "In the new Wolfram Language we implemented this new kind of thing or as we called it complexity speed-up... the harder your problems get, the faster Mathematica will solve them!" $\endgroup$ Commented Jul 15, 2014 at 1:50
  • 3
    $\begingroup$ I didn't dare to post my SunPosition is horribly slow rant here and used Wolfram Community. :) $\endgroup$ Commented Jul 15, 2014 at 5:51
  • 1
    $\begingroup$ When you first posted this, I wrote a variant of your code using GroupBy, it is a bit slower than yours, but it is nice and succinct: posIdx[x_] := GroupBy[Range@Length@x, (x[[#]] &) -> Identity]. $\endgroup$ Commented Jul 15, 2014 at 12:56
  • 3
    $\begingroup$ Note that PositionIndex does work correctly with held expressions, whereas this is a bit painful to implement using GatherBy. a = 1; PositionIndex[Unevaluated[{a, b, c, d}]] $\endgroup$ Commented Jul 15, 2014 at 14:51
  • 3
    $\begingroup$ The performance has improved considerably in v10.0.1.0, but your myPosIdx is still slightly faster. $\endgroup$ Commented Sep 17, 2014 at 8:35

3 Answers 3

Reset to default
42
$\begingroup$

First let me note that I didn't write PositionIndex, so I can't speak to its internals without doing a bit of digging (which at the moment I do not have time to do).

I agree performance could be improved in the case where there are many collisions. Let's quantify how bad the situation is, especially since complexity was mentioned!

We'll use the benchmarking tool in GeneralUtilities to plot time as a function of the size of the list:

Needs["GeneralUtilities`"] myPosIdx[x_] := <|Thread[x[[#[[All, 1]]]] -> #]|> &@ GatherBy[Range@Length@x, x[[#]] &]; BenchmarkPlot[{PositionIndex, myPosIdx}, RandomInteger[100, #] &, 16, "IncludeFits" -> True]

which gives:

PositionIndex benchmark

While PositionIndex wins for small lists (< 100 elements), it is substantially slower for large lists. It does still appear to be $O(n \log n)$, at least.

Let's choose a much larger random integer (1000000), so that we don't have any collisions:

enter image description here

Things are much better here. We can see that collisions are the main culprit.

Now lets see how the speed for a fixed-size list depends on the number of unique elements:

BenchmarkPlot[{PositionIndex, myPosIdx}, RandomInteger[#, 10^4] &, 2^{3, 4, 5, 6, 7, 8, 9, 10, 11, 12}]

enter image description here

Indeed, we can see that PositionIndex (roughly) gets faster as there are more and more unique elements, whereas myPosIdx gets slower. That makes sense, because PositionIndex is probably appending elements to each value in the association, and the fewer collisions the fewer (slow) appends will happen. Whereas myPosIdx is being bottlenecked by the cost of creating each equivalence class (which PositionIndex would no doubt be too, if it were faster). But this is all academic: PositionIndex should be strictly faster than myPosIdx, it is written in C.

We will fix this.

Improve this answer
$\endgroup$
7
  • $\begingroup$ I look forward to seeing this improved - as bad as it is with the user-side GatherBy implementation, it's even worse off against this $\endgroup$ Commented Jul 15, 2014 at 4:31
  • 2
    $\begingroup$ Would love to learn more about GeneralUtilities` . $\endgroup$ Commented Jul 15, 2014 at 4:34
  • 1
    $\begingroup$ @Szabolcs ?GeneralUtilities*` ... Many functions have a brief synopsis or code. $\endgroup$ Commented Jul 15, 2014 at 5:22
  • $\begingroup$ Thanks again for taking the time to answer one of my Questions, even one as discourteous as this. Thank you also for the analysis. I was aware of cases where PositionIndex appears more favorable but as you said the bottom line is: "PositionIndex should be strictly faster than myPosIdx (since) it is written in C." Also your point about complexity is taken, but if I am not mistaken computational complexity is multidimensional: it is not merely about e.g. list length but also other factors (e.g. number of unique elements), therefore I stand by my statement that it has poor complexity. $\endgroup$ Commented Jul 15, 2014 at 6:08
  • 1
    $\begingroup$ Anyway, thanks again for your attention and affirmation that this will be corrected. $\endgroup$ Commented Jul 15, 2014 at 6:09
8
$\begingroup$

rcollyer pointed out in a comment that the the new GroupBy may be substituted for GatherBy in Szabolcs's original to produce the desired function:

cleanPosIdx[x_] := GroupBy[Range @ Length @ x, x[[#]] &]

I shall be using this code until PositionIndex receives an enhancement.

Improve this answer
$\endgroup$
5
$\begingroup$

Here's an alternative using the "GroupByList" resource function:

pIndex[i_List] := ResourceFunction["GroupByList"][Range @ Length @ i, i]

Comparison:

a = RandomInteger[10, 10^6]; r1 = pIndex[a]; //RepeatedTiming r2 = myPosIdx[a]; //RepeatedTiming r3 = PositionIndex[a]; //RepeatedTiming r1 === r2 === r3

{0.02, Null}

{0.043, Null}

{0.11, Null}

True

Improve this answer
$\endgroup$
1
  • $\begingroup$ I don't have ResourceFunction in v10.1. Why not provide an implementation using the GatherByList code you already posted? $\endgroup$ Commented Dec 9, 2019 at 17:36

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.