2
$\begingroup$

So I'm trying to fit experimental data to a nonlinear model using the NonLinearModelFit command, but it isn't quite working.

The plotted data set looks like this:

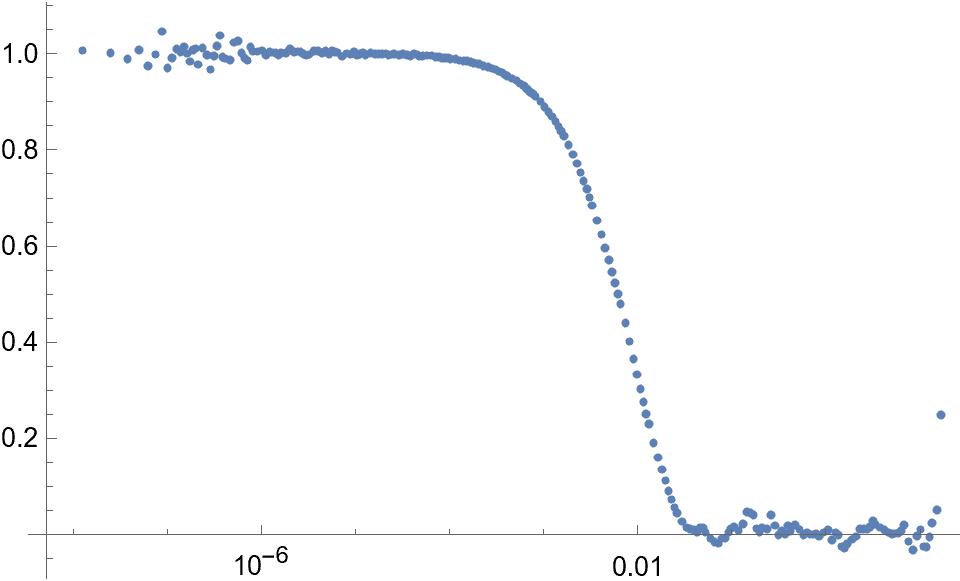
The data is to be fitted with

1+β*exp⁡(-2γ*t),

so I tried using the NonLinearModelFit command as follows:

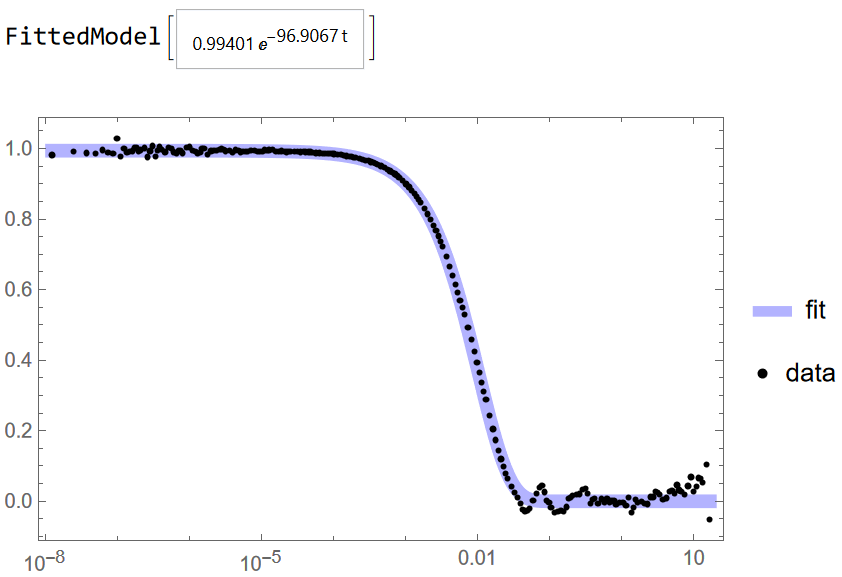
nlm = NonlinearModelFit[data, 1 + beta*Exp[-2 gamma*t], {beta, gamma}, t]; LogLinearPlot[nlm[t], {t, 0, data[[Length[data], 1]]}, PlotRange -> Automatic] Show[ListLogLinearPlot[data], LogLinearPlot[nlm[t], {t, 0, data[[Length[data], 1]]}, PlotStyle -> Red]]

which looks like

The proposed function obviously doesn't fit the data set and is a scaled down version shifted to the right, without the last almost constant part of the data.

What's happening here? How can I accurately fit the data and maybe use some initial values for the parameters β and γ?

The data used to plot and fit:

082222 1251 PM Experiment Type Sizing Pseudo Cross Correlation Scattering angle 40.0 Duration (s) 20 Wavelength (nm) 660.0 Refractive index 1.330 Viscosity (mPas) 1.000 Temperature (K) 293.2 Laser intensity (mW) 0.147463 Average Count rate A (kHz) 191.3 Average Count rate B (kHz) 192.1 Intercept 0.9941 Cumulant 1st 667.97 Cumulant 2nd 667.97 0.00 Cumulant 3rd 641.63 0.40 Lag time (s) g2-1 1.250000E-8 0.981694 2.500000E-8 0.991310 3.750000E-8 0.987267 5.000000E-8 0.986830 6.250000E-8 0.995900 7.500000E-8 0.988141 8.750000E-8 0.985300 1.000000E-7 1.028684 1.125000E-7 0.977760 1.250000E-7 1.000162 1.375000E-7 0.988360 1.500000E-7 0.991529 1.625000E-7 0.992731 1.750000E-7 1.001255 1.875000E-7 1.003659 2.000000E-7 0.992731 2.125000E-7 0.996173 2.375000E-7 1.001583 2.625000E-7 0.976339 2.875000E-7 0.992731 3.125000E-7 1.007101 3.375000E-7 0.977377 3.625000E-7 0.994370 3.875000E-7 1.004151 4.125000E-7 0.997539 4.625000E-7 0.989972 5.125000E-7 1.003577 5.625000E-7 1.000408 6.125000E-7 0.990054 6.625000E-7 0.985109 7.125000E-7 0.992977 7.625000E-7 0.994452 8.125000E-7 0.987171 9.125000E-7 1.003509 1.012500E-6 1.004055 1.112500E-6 0.994712 1.212500E-6 0.990600 1.312500E-6 0.985559 1.412500E-6 0.988237 1.512500E-6 1.000039 1.612500E-6 1.001002 1.812500E-6 0.983599 2.012500E-6 0.993154 2.212500E-6 0.994131 2.412500E-6 0.994090 2.612500E-6 0.997109 2.812500E-6 0.998311 3.012500E-6 0.997553 3.212500E-6 0.993281 3.612500E-6 0.994408 4.012500E-6 0.989310 4.412500E-6 0.996071 4.812500E-6 0.993520 5.212500E-6 0.990286 5.612500E-6 0.992212 6.012500E-6 0.992093 6.412500E-6 0.992017 7.212500E-6 0.994756 8.012500E-6 0.994418 8.812500E-6 0.991991 9.612500E-6 0.990677 1.041250E-5 0.991290 1.121250E-5 0.995478 1.201250E-5 0.993559 1.281250E-5 0.996065 1.441250E-5 0.996347 1.601250E-5 0.991484 1.761250E-5 0.990913 1.921250E-5 0.993117 2.081250E-5 0.991552 2.241250E-5 0.990403 2.401250E-5 0.991326 2.561250E-5 0.991138 2.881250E-5 0.991134 3.201250E-5 0.991837 3.521250E-5 0.990236 3.841250E-5 0.990808 4.161250E-5 0.989931 4.481250E-5 0.990017 4.801250E-5 0.990026 5.121250E-5 0.988744 5.761250E-5 0.987654 6.401250E-5 0.987021 7.041250E-5 0.986750 7.681250E-5 0.985235 8.321250E-5 0.985939 8.961250E-5 0.985592 9.601250E-5 0.985029 0.000102 0.984424 0.000115 0.982993 0.000128 0.982606 0.000141 0.980761 0.000154 0.978720 0.000166 0.978311 0.000179 0.977051 0.000192 0.975604 0.000205 0.974399 0.000230 0.972358 0.000256 0.969710 0.000282 0.966684 0.000307 0.965229 0.000333 0.961571 0.000358 0.960360 0.000384 0.957262 0.000410 0.955180 0.000461 0.950771 0.000512 0.945581 0.000563 0.941056 0.000614 0.936345 0.000666 0.931493 0.000717 0.927869 0.000768 0.922947 0.000819 0.918401 0.000922 0.908841 0.001024 0.899845 0.001126 0.890876 0.001229 0.881773 0.001331 0.873013 0.001434 0.864277 0.001536 0.855824 0.001638 0.847578 0.001843 0.830522 0.002048 0.814198 0.002253 0.798193 0.002458 0.782513 0.002662 0.767277 0.002867 0.752026 0.003072 0.736805 0.003277 0.721951 0.003686 0.693111 0.004096 0.665850 0.004506 0.640100 0.004915 0.615177 0.005325 0.591402 0.005734 0.569494 0.006144 0.548935 0.006554 0.529993 0.007373 0.493404 0.008192 0.458930 0.009011 0.425248 0.009830 0.394020 0.010650 0.364432 0.011469 0.337440 0.012288 0.311853 0.013107 0.287955 0.014746 0.243217 0.016384 0.205101 0.018022 0.173352 0.019661 0.144798 0.021299 0.120097 0.022938 0.098263 0.024576 0.079198 0.026214 0.064734 0.029491 0.041283 0.032768 0.024546 0.036045 0.009757 0.039322 -0.007328 0.042598 -0.023800 0.045875 -0.027768 0.049152 -0.025468 0.052429 -0.020721 0.058982 0.002437 0.065536 0.022033 0.072090 0.038237 0.078643 0.044000 0.085197 0.025870 0.091750 0.002250 0.098304 -0.003367 0.104858 -0.018009 0.117965 -0.031016 0.131072 -0.029388 0.144179 -0.026414 0.157286 -0.028317 0.170394 -0.016462 0.183501 0.007269 0.196608 0.010597 0.209715 0.015417 0.235930 0.019428 0.262144 0.020318 0.288358 0.032608 0.314573 0.035763 0.340787 0.022082 0.367002 -0.006260 0.393216 0.004914 0.419430 0.007707 0.471859 -0.005449 0.524288 0.006633 0.576717 -0.004173 0.629146 0.007739 0.681574 -0.001696 0.734003 0.000670 0.786432 0.001787 0.838861 -0.009630 0.943718 -0.003229 1.048576 -0.003674 1.153434 -0.011465 1.258291 0.010513 1.363149 -0.031880 1.468006 -0.017126 1.572864 0.004514 1.677722 -0.003074 1.887437 0.000161 2.097152 -0.005843 2.306867 -0.007362 2.516582 0.012358 2.726298 0.011785 2.936013 0.028037 3.145728 0.024937 3.355443 0.019830 3.774873 0.004959 4.194304 0.009447 4.613734 0.028008 5.033165 0.031347 5.452595 0.021929 5.872025 0.046492 6.291456 0.031570 6.710886 0.027511 7.549747 0.018476 8.388608 0.043572 9.227468 0.068573 10.066330 0.027640 10.905190 0.042270 11.744051 0.065827 12.582912 0.064546 13.421773 0.053715 15.099494 0.105235 16.777216 -0.051853
Improve this question
$\endgroup$
2
  • $\begingroup$ I haven't tried fitting your data. Have you drop parts of the data apparently not fitting into 1+β*exp⁡(-2γ*t), say the tails. $\endgroup$ Commented Sep 11, 2022 at 19:18
  • $\begingroup$ I tried excluding the plotpoints with t<10^-6, but it just shifted the fitted function a tiny bit in negative y direction $\endgroup$ Commented Sep 11, 2022 at 19:27

1 Answer 1

Reset to default
6
$\begingroup$

I think your proposed model may be inappropriate for your data. The main trend in your data is a simple exponential decay, a model that fits remarkably well:

nlm = NonlinearModelFit[data, beta Exp[-gamma t], {{beta, 1}, {gamma, 100}}, t] Show[ LogLinearPlot[ Legended[nlm[t], "fit"], {t, data[[1, 1]], data[[-1, 1]]}, Frame -> True, Axes -> False, PlotRange -> All, PlotStyle -> Directive[Opacity[0.3, Blue], Thickness[0.02]] ], ListLogLinearPlot[Legended[data, "data"], PlotStyle -> Black] ]

fit and original data on log-linear plot

data comes from data = ImportString[" your data table minus the headers ", "Table"].

Improve this answer
$\endgroup$
3
  • $\begingroup$ Thank very much, I've been sitting on this the whole day :D $\endgroup$ Commented Sep 11, 2022 at 20:51
  • $\begingroup$ may I ask how you picked the initial values for gamma and beta? $\endgroup$ Commented Sep 11, 2022 at 21:31
  • 1
    $\begingroup$ @xPigeonDestroyer2000 Beta is easy: for $t=0 $ the model reduces to $\beta\ e^0 = \beta$ and this value should correspond to the initial value of the data, which is around 1, so $\beta = 1$ is a good starting point. For $\gamma$, it was just trial and error. $\endgroup$ Commented Sep 11, 2022 at 23:24

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.