11
$\begingroup$

I need to do the following:

  1. Define a function
  2. Take the derivative of this function and have a look at the symoblic representation
  3. Substitute in some values

With the bonus that I want to use the correct variable names everywhere to not mess up my head. So I have defined:

a = 0.04; L1 = 1; L0 = 1;

My function being

L[s_, L0_, L1_, a_] := L1 + L0/(1 + s/a);

I don't know how to easily take the derivative of this expression when the arguments are defined (and I don't want to make up new variable names). The best way I could find was using module, like this:

Module[{s, L0, L1, a}, D[L[s, L0, L1, a], s]]

But this had an unexpected result,

$-\frac{\text{L0$\$$7293}}{\text{a$\$$7293} \left(1+\frac{\text{s$\$$7293}}{\text{a$\$$7293}}\right)^2}$

I can't figure out where $7293 comes from? Also, is there a better way, perhaps a way so that I don't have to specify the variables I want to localize? Just telling Mathematica, "do this symbolically".

Improve this question
$\endgroup$
3
  • 1
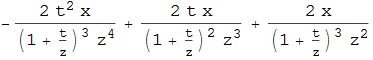
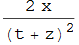
    $\begingroup$ In this particular example D[L[s, L0, L1, a], s] is sufficient because s has no value. Or do you mean don't want to substitute in the values for L0, etc. at all? In that case I suggest you don't give them values. Make a rule list instead pars = {a -> 0.04, L1 -> 1, L0 -> 1}, and do expr /. pars when you need to substitute them into expr. $\endgroup$ Commented May 11, 2012 at 7:44
  • 1
    $\begingroup$ If you go with the approach I suggested, please see this as well. $\endgroup$ Commented May 11, 2012 at 7:46
  • $\begingroup$ Ah... yes, substituting values with expr /. pars is a lot better. I was looking for something like this, I assume it will solve my $-problem to so if you post this I will accept it as an answer. $\endgroup$ Commented May 11, 2012 at 7:48

3 Answers 3

Reset to default
15
$\begingroup$

If you need to work with a set of variables symbolically, but you also need to substitute in values for them occasionally, a good approach is to use a rule list:

values = {a -> 0.04, L1 = 1, L0 -> 1}

If the symbols have no values assigned, you can use them normally in symbolic calculations:

L[s_, L0_, L1_, a_] := L1 + L0/(1 + s/a) D[L[s, L0, L1, a], s] (* ==> -(L0/(a (1 + s/a)^2)) *)

When you need to substitute in numerical values, use ReplaceAll:

D[L[s, L0, L1, a], s] /. values (* ==> -(25./(1 + 25. s)^2) *)

I wrote a bit more about using parameter list (rule lists) in this answer.

Improve this answer
$\endgroup$
26
$\begingroup$

There is no need to play around with ReplaceAll, Rule, Block, Module or whatever using D, since you have an oparator Derivative really fulfilling your needs while you need not bother if the arguments were defined, so I recommend it to find symbolic derivatives of your function. Remember of shorthands f', f'' to represent first and second derivatives of one-variable functions, e.g. Cos' returns the result as a pure function : -Sin[#1] &, so Derivative acts as an operator on functions, but you can still evaluate it for an argument or even more - you can find n-th indefinite integral of the original function if you evaluate Derivative[-n][f], e.g. :

FullForm /@ {f', f'''[x], f''} Derivative[-5][Cos][x] Derivative[-3][#^2 - 2 # + 1 &][x] 
{Derivative[1][f], Derivative[3][f][x], Derivative[2][f]} Sin[x] x^3/6 - x^4/12 + x^5/60

Use it this way to find the first derivative of L with respect to s :

Derivative[1, 0, 0, 0][L][s, L0, L1, a] 
 -(L0/(a (1 + s/a)^2)) 
Derivative[1, 0, 0, 0][L][t, x, y, z] // Simplify 
 -((x z)/(t + z)^2) 
a = 0.04; L1 = 1; L0 = 1; Derivative[1, 0, 0, 0][L][s, L0, L1, a] 
-(25./(1 + 25. s)^2)

let's define something more general, e.g. d'Alembertian of a function f :

dAl[f_][t_, x_, y_, z_] := Derivative[2, 0, 0, 0][f][t, x, y, z] - Derivative[0, 2, 0, 0][f][t, x, y, z] - Derivative[0, 0, 2, 0][f][t, x, y, z] - Derivative[0, 0, 0, 2][f][t, x, y, z]

for your function this yields :

dAl[L][t, x, y, z] % // Simplify

enter image description here

enter image description here

and 

dAl[L][s, L0, L1, a] // Simplify 
(1250. + 31250. s)/(1. + 25. s)^3
Improve this answer
$\endgroup$
2
  • $\begingroup$ That's the most systematic approach (+1). $\endgroup$ Commented May 11, 2012 at 13:55
  • $\begingroup$ @Jens I think that Derivative is really unappreciated by most of the Mathematica users. Thanks for an upvote. $\endgroup$ Commented May 11, 2012 at 14:42
14
$\begingroup$

While the answer of Szabolcs is clearly the best alternative, if you have already assigned values to the variables and clearing them for some reason is no viable option, you can use

Block[{s, L0, L1, a}, Hold@Evaluate@D[L[s, L0, L1, a], s]]

Unlike Module, Block doesn't introduce new variable names but temporarily removes the values of those given. Hold prevents Mathematica from inserting the values after return (otherwise you'd get the numerical value of the derivative for the assigned values; if that's what you want, just omit the Hold@Evaluate@), and Evaluate ensures that the expression is evaluated inside the Block despite of the Hold.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.