78
$\begingroup$

It is known that space curves can either be defined parametrically,

$$\begin{align*}x&=f(t)\\y&=g(t)\\z&=h(t)\end{align*}$$

or as the intersection of two surfaces,

$$\begin{align*}F(x,y,z)&=0\\G(x,y,z)&=0\end{align*}$$

Curves represented parametrically can of course be plotted in Mathematica using ParametricPlot3D[]. Though implicitly-defined plane curves can be plotted with ContourPlot[], and implicitly-defined surfaces can be plotted with ContourPlot3D[], no facilities exist for plotting space curves like the intersection of the torus $(x^2+y^2+z^2+8)^2=36(x^2+y^2)$ and the cylinder $y^2+(z-2)^2=4$:

torus-cylinder intersection

Sometimes, one might be lucky and manage to find a parametrization for the intersection of two algebraic surfaces, but these situations are few and far between, especially if the two surfaces are of sufficiently high degree. The situation is worse if at least one of the surfaces is transcendental.

How might one write a routine that plots space curves defined as the intersection of two implicitly-defined surfaces?

It would be preferable if the routine returns only Line[] objects representing the space curve. A routine that handles only algebraic surfaces would be an acceptable answer, but it would be nice if your routine can handle transcendental surfaces as well. A bonus feature for the routine might be the ability to determine if the two surfaces given do not have a space curve intersection, or intersect only at a single point, or other such degeneracies.

Improve this question
$\endgroup$
9
  • 3
    $\begingroup$ Finally, I'll be able to properly intersect the columns with the roof $\endgroup$ Commented May 23, 2012 at 20:18
  • $\begingroup$ @R.M, Funny, I thought getting the intersection of two parametrically-defined surfaces was an even tougher problem... so I decided not to ask for it in the question. :) That would be nice, though. $\endgroup$ Commented May 23, 2012 at 20:25
  • $\begingroup$ @J. M.♦ Can we extend the question a bit by considering intersection of two BSpline surfaces that has no explicit analytical form? This will be very effective for 3D modeling. $\endgroup$ Commented May 23, 2012 at 21:28
  • $\begingroup$ @Plato: that might be best done as a separate question... (that would be covered by the "two parametrically-defined surfaces" case, as BSplineSurface[] objects can be transformed into BSplineFunction[]s). $\endgroup$ Commented May 23, 2012 at 21:36
  • 2
    $\begingroup$ @rcollyer Regarding the equation: if you accept a differential equation then it's easy: take the cross product of the gradients of the implicit functions, and perhaps normalize it (call it t[r], where r is a 3D point). Then the curve is described by D[r[u],u] == t[r[u]] for curve parameter u. This is because t must be tangent to both surfaces for all points r on the intersection curve. You "just" have to integrate that equation with a starting point r0 on the intersection. $\endgroup$ Commented May 24, 2012 at 3:26

4 Answers 4

Reset to default
75
$\begingroup$

I take zero credit for this. It is a method I learned from Maxim Rytin.

ContourPlot3D[{(x^2 + y^2 + z^2 + 8)^2 - 36 (x^2 + y^2), y^2 + (z - 2)^2 - 4}, {x, -4, 4}, {y, -4, 4}, {z, -2, 2}, Contours -> {0}, ContourStyle -> Opacity[0], Mesh -> None, BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> {{Green, Tube[.03]}}}, Boxed -> False]

torus-cylinder intersection

Improve this answer
$\endgroup$
5
  • 6
    $\begingroup$ +1 Magical ;-) {1,2}->Green means intersection (boundary) between surface 1 and 2 will be green. Here is a minimal set of options to make it work: ContourPlot3D[{(x^2 + y^2 + z^2 + 8)^2 - 36 (x^2 + y^2), y^2 + (z - 2)^2 - 4}, {x, -4, 4}, {y, -4, 4}, {z, -2, 2}, ContourStyle -> None, Mesh -> None, BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> Green}] $\endgroup$ Commented May 23, 2012 at 22:28
  • $\begingroup$ Nice! I find it interesting, though, that the docs do not say that the Filling format specification can be applied to BoundaryStyle. Very useful. $\endgroup$ Commented May 24, 2012 at 3:01
  • $\begingroup$ I'll just note that if you take a look at the InputForm[] of the output of Daniel's version, the Polygon[] objects representing the isosurfaces are still there, just transparent. One could of course do something like ContourPlot3D[{(x^2 + y^2 + z^2 + 8)^2 - 36 (x^2 + y^2), y^2 + (z - 2)^2 - 4}, {x, -4, 4}, {y, -4, 4}, {z, -2, 2}, BoundaryStyle -> {1 -> None, 2 -> None, {1, 2} -> {}}, ContourStyle -> None, Mesh -> None] (as Vitaliy comments) if one just wants the curves themselves. So many unused points, though... $\endgroup$ Commented May 24, 2012 at 5:49
  • $\begingroup$ @J. M. Thanks for the updates. I seem to be getting an awful lot of upvotes for code that was never of my own devising, and not notably better (that I can tell) than that in the other response. Embarrassed am I. $\endgroup$ Commented May 24, 2012 at 14:22
  • 1
    $\begingroup$ As rightly you should be keeping all the geometric goodies to yourself. There should be a spelunking tag… $\endgroup$ Commented Sep 17, 2012 at 8:33
40
$\begingroup$

This is admittedly a hack, and does not work as well with PlotPoints / MaxRecursion as a dedicated function would (you will notice that I needed to increase PlotPoints for a good result), but it's a good way to make a quick and dirty plot:

ContourPlot3D[(x^2 + y^2 + z^2 + 8)^2 == 36 (x^2 + y^2), {x, -4, 4}, {y, -4, 4}, {z, -2, 2}, MeshFunctions -> {Function[{x, y, z}, y^2 + (z - 2)^2 - 4]}, Mesh -> {{0}}, ContourStyle -> None, PlotPoints -> 30, BoxRatios -> Automatic]

Mathematica graphics

Addendum

Per @whuber's comment below, the same thing can be achieved using RegionFunction:

ContourPlot3D[(x^2 + y^2 + z^2 + 8)^2 == 36 (x^2 + y^2), {x, -4, 4}, {y, -4, 4}, {z, -2, 2}, RegionFunction -> Function[{x, y, z}, y^2 + (z - 2)^2 < 4], ContourStyle -> None, Mesh -> None, BoxRatios -> Automatic]

The style can be adjusted using BoundaryStyle.

I believe that this will give good quality results even without increasing PlotPoints, but I'll need to do some more testing before I can be certain about that...

Improve this answer
$\endgroup$
6
  • $\begingroup$ What made this problem hard back in the days of old Mathematica was that the version of ContourPlot3D[] available in the standard packages didn't have the MeshFunctions option, and thus it took a bit of labor to look at which polygons were intersecting. This is nice, even if it is quick-and-dirty. :) $\endgroup$ Commented May 23, 2012 at 20:29
  • $\begingroup$ +1 With suitable graphics settings, the RegionFunction option will accomplish something similar. $\endgroup$ Commented May 23, 2012 at 20:32
  • $\begingroup$ @J.M. I think Mathematica's plotting framework is really powerful, and it uses adaptive sampling at every stage. I am not sure if mesh lines are computed with a higher resolution than the surface or not, but the system definitely has the capability to do this for the intersection of two surfaces: it does it when computing exclusions. Try e.g. Plot3D[Boole[x^2 + y^2 < 1], {x, -1.1, 1.1}, {y, -1.1, 1.1}] and note how smooth and sharp the circle boundary is. If you turn off exclusions (Exclusions -> None), it'll be a lot more jagged. $\endgroup$ Commented May 23, 2012 at 20:33
  • $\begingroup$ @whuber And you just answered the question that didn't fit in the comment I wrote above! RegionFunction will sample the intersection curve very smoothly, similarly to how Exclusions are computed! (The Plot example above.) This should give a better result than MeshFunctions, I think, but I'd need to test it. $\endgroup$ Commented May 23, 2012 at 20:34
  • $\begingroup$ +1. With Mesh -> All, PlotStyle -> None, PlotPoints -> 3 you'll see the possibly pre-generated smooth circle boundary. $\endgroup$ Commented Jun 17, 2015 at 6:57
35
$\begingroup$

Introduction

I worked up my solution and then saw that Jens had suggested this approach in a comment. Well, here's my approach. It is fairly general. I made no attempt to determine how many connected components there are and finding parametrizations of each one.

  1. Find a point on the intersection. This could be a difficult step, depending on how much is known about the surfaces.

    • A known point.
    • Use Solve or NSolve, if they work. One might be able to solve one variable in terms of the others or use a hyperplane that intersects the intersection of the surfaces.
    • Use root-finding, provided a feasible starting point is known. I'll give a pseudo-Newton's Method function for hunting down an intersection point below.

  2. Integrate the normalized cross product of the gradients of the function {f, g} that define the surfaces {f == 0, g == 0}. Since the cross product is perpendicular to both gradients of f and g, it will be tangent to the intersection curve. Using the normalized vector yields a unit-speed parametrization. This is fairly easy with NDSolve.

    • Determining the limits of integration usually needs some user-input.
    • We can get a periodic interpolation of closed curves.

Utility functions

findPoint[{f, g}, {{x, y, z}, {x0, y0, z0}}] - finds a point on the intersection of {f == 0, g == 0}, starting at {x0, y0, z0}. It uses Newton-Method-like step pseudonewton.

periodicEvent[v, v0, p0] - stops integration when the solution has completed a loop, using the condition v == v0 to trigger the event; p0 should be the initial point and v0 should be the corresponding coordinate.

findIntersection3D[{f, g}, {{x, y, z}, {x0, y0, z0}}, {t, t1, t2}] - finds a parametrization of the intersection of {F == 0, g == 0} near the point {x0, y0, z0}.

periodicReinterpolation[if] - converts the InterpolatingFunction if to a periodic one. Just something "extra"; it plays no crucial role.

showall[{f, g}, sol] - another "extra," which shows the plots of f == 0, g == 0, and the intersection parametrized by sol.

Examples

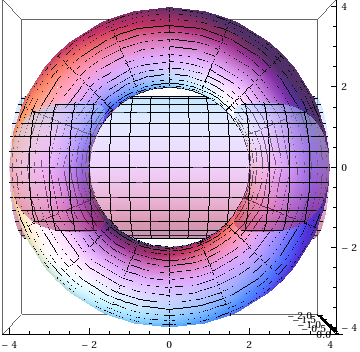
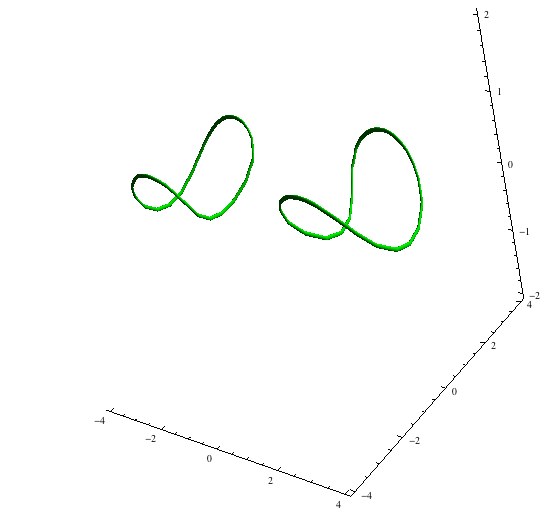
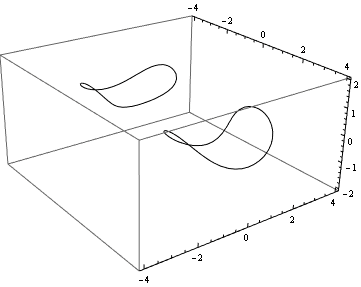
The three examples below were each shown with showall[{f, g}, sol].

OP's example. Converting to a periodic interpolation is not necessary; it is done merely to show it can be done.

{f, g} = {(x^2 + y^2 + z^2 + 8)^2 - 36 (x^2 + y^2), y^2 + (z - 2)^2 - 4}; sol = findIntersection3D[{f, g}, {{x, y, z}, #}, {t, 0, 100}, "EventFunctions" -> {periodicEvent[y[t], #[[2]], #] &}] & /@ {{-4, 0, 0}, {4, 0, 0}} /. if_InterpolatingFunction :> periodicReinterpolation[if];

Helix. OK, paramterization by hand is easy, but I've always liked this construction of the helix as the intersection of two corrugated sheets. I used Solve to find the point of intersection at the bottom of the plot range (z == -4). It's actually shorter to write it out explicitly, but in principle

{f, g} = {x - Cos[2 z], y - Sin[2 z]}; sol = findIntersection3D[{f, g}, {{x, y, z}, {x, y, z} /. First@Solve[{z == -4, {x - Cos[2 z], y - Sin[2 z]} == {0, 0}}}, {t, 0, 100}, "EventFunctions" -> {WhenEvent[z[t] == 4, "StopIntegration"] &}];

A somewhat random transcendental surface and sphere.

{f, g} = {x + Sin[y] + Cos[2 z], x^2 + y^2 + z^2 - 9}; sol = findIntersection3D[{f, g}, {{x, y, z}, {0, 0, 2}}, {t, 0, 100}, "EventFunctions" -> {periodicEvent[x[t], First[#], #] &}];

Mathematica graphics

Code

Root-finding. I have not seen Newton's Method used on an underdetermined system, but that's basically that findPoint does. In the main function, findPoint starts the search at the point {x0, y0, z0} passed to findIntersection3D.

ClearAll[findPoint, pseudonewton, periodicEvent, findIntersection3D, periodicReinterpolation, showall]; pseudonewton[f_List, {x_, y_, z_}] := pseudonewton[f, D[f, {{x, y, z}}], {x, y, z}]; pseudonewton[f_List, df_?MatrixQ, {x_, y_, z_}] := With[{df0 = df /. Thread[{x, y, z} -> #], f0 = f /. Thread[{x, y, z} -> #]}, # - PseudoInverse[df0].f0] &; findPoint[f_List, {{x_, y_, z_}, {x0_, y0_, z0_}}] := NestWhile[pseudonewton[f, D[f, {{x, y, z}}], {x, y, z}], {x0, y0, z0}, Norm[f /. Thread[{x, y, z} -> #]] > 1*^-15 &, 2, 100];

Constructing the intersection. Although one specifies an interval {t, t1, t2} in calling findIntersection3D (see above, Utility functions), events are probably the easiest way to control the interval of integration. The option "EventFunctions" -> list takes a list of functions whose input is the starting point found by findPoint. They should output an WhenEvent expression. The function periodicEvent returns a event function that detects when the path computed by NDSolve returns to its starting position. When the variable v equals the number v0 and the point {x[t], y[t], z[t]}, is close to the starting point p0, integration stops; the number v0 should be the corresponding coordinate of p0. In certain cases, periodicEvent might need tweaking. The condition that the distance be within 0.1 is coordinated with the option MaxStepSize -> 0.1 in NDSolve. If the step size is greater, the event may be missed. It can also happen that the starting point p0 is at an extreme value of the variable v that periodicEvent tracks. Either change the variable or pass a periodicEvent for two or three variables.

periodicEvent[v_, v0_, p0_] := WhenEvent[v == v0 && Norm[{x[t], y[t], z[t]} - p0] < 0.1, "StopIntegration"]; Options[findIntersection3D] = Join[{"EventFunctions" -> {}}, Options[NDSolve]]; findIntersection3D[funcs : {_, _}, {{x_, y_, z_}, {x0_, y0_, z0_}}, {t_, t1_, t2_}, opts : OptionsPattern[]] := Module[{vel, eqn, ics, invariants}, vel = Cross @@ D[funcs, {{x, y, z}}] // Normalize; eqn = {x'[t], y'[t], z'[t]} == (vel /. {v : x | y | z :> v[t]}); ics = findPoint[funcs, {{x, y, z}, N@{x0, y0, z0}}]; invariants = funcs /. {v : x | y | z :> v[t]}; First@NDSolve[{ eqn, {x[0], y[0], z[0]} == ics, Through[OptionValue["EventFunctions"][ics]]}, {x, y, z}, {t, 0, 100}, FilterRules[{opts}, Options[NDSolve]], MaxStepSize -> 0.1, Method -> {"Projection", "Invariants" -> invariants}] ];

Extras.

showall[{f_, g_}, sol_] := Show[ ContourPlot3D[{f == 0, g == 0}, {x, -4, 4}, {y, -4, 4}, {z, -4, 4}, ContourStyle -> Opacity[0.5], Mesh -> None], ParametricPlot3D[{x[t], y[t], z[t]} /. sol // Evaluate, Evaluate@Join[{t}, Flatten[x["Domain"] /. First@sol]], PlotStyle -> Black] ]; periodicReinterpolation[if_InterpolatingFunction] := Module[{coords = First@if["Coordinates"], values = if["ValuesOnGrid"]}, If[Chop@First@Differences[if /@ Flatten[if["Domain"]]] != 0, Print["Warning: The endpoints are significantly different."]]; values[[-1]] = values[[1]]; Interpolation[Transpose@{coords, values}] ];
Improve this answer
$\endgroup$
3
  • $\begingroup$ Looks great. I'll test this when I have Mathematica access again. $\endgroup$ Commented May 2, 2015 at 3:03
  • $\begingroup$ Finally tried it out (after making a few modifications to use Method -> "EventLocator" instead); it works nicely for nonsingular curves. Two things: why not use LeastSquares[] for pseudonewton[]; and, have you already seen this? $\endgroup$ Commented Aug 28, 2015 at 11:52
  • $\begingroup$ @J.M. I might have forgotten or not know about LeastSquares; or because I think of Newton's method in terms of "dividing by the derivative" and PseudoInverse expresses that idea. Testing LeastSquares, it seems slightly slower but that's hardly important here. I probably saw the article in 1998, but I didn't remember it. Thanks. $\endgroup$ Commented Aug 29, 2015 at 15:03
16
$\begingroup$

After version 10, using mesh-based geometric regions, it's become simpler

reg = ImplicitRegion[(x^2 + y^2 + z^2 + 8)^2 == 36 (x^2 + y^2) && y^2 + (z - 2)^2 == 4, {x, y, z}]; disReg = DiscretizeRegion[reg] Graphics3D[{Red, MeshPrimitives[disReg, 1]}]

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.