Borrowing almost verbatim from a recent response about finding extremaextrema, here is a method that is useful when your function is differentiable and hence can be "tracked" by NDSolve.
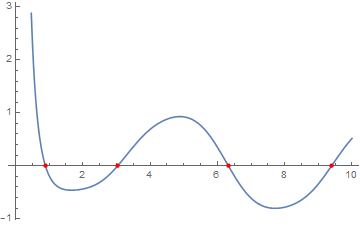
f[x_] := BesselJ[1, x]^2 + BesselK[1, x]^2 - Sin[Sin[x]] In[191]:= zeros = Reap[soln = y[x] /. First[ NDSolve[{y'[x] == Evaluate[D[f[x], x]], y[10] == (f[10])}, y[x], {x, 10, 0}, Method -> {"EventLocator", "Event" -> y[x], "EventAction" :> Sow[{x, y[x]}]}]]][[2, 1]] During evaluation of In[191]:= NDSolve::mxst: Maximum number of 10000 steps reached at the point x == 1.5232626281716416`*^-124. >> Out[191]= {{9.39114, 8.98587*10^-16}, {6.32397, -3.53884*10^-16}, {3.03297, -8.45169*10^-13}, {0.886605, -4.02456*10^-15}} Plot[f[x], {x, 0, 10}, Epilog -> {PointSize[Medium], Red, Point[zeros]}] 
If it were a trickier function, one might use Method -> {"Projection", ...} to enforce the condition that y[x] is really the same as f[x]. This method may be useful in situations (if you can find them) where we have one function in one variable, and Reduce either cannot handle it or takes a long time to do so.
Addendum by J. M.
WhenEvent is now the documented way to include event detection in NDSolve, so using it along with the trick of specifying an empty list where the function should be, here's how to get a pile of zeroes:
f[x_] := BesselJ[1, x]^2 + BesselK[1, x]^2 - Sin[Sin[x]] zeros = Reap[NDSolve[{y'[x] == D[f[x], x], WhenEvent[y[x] == 0, Sow[{x, y[x]}]], y[10] == f[10]}, {}, {x, 10, 0}]][[-1, 1]]; Plot[f[x], {x, 0, 10}, Epilog -> {PointSize[Medium], Red, Point[zeros]}]