I have this code:
K[Q_, n_Integer] := Module[{z, x}, SymmetricReduction[ SeriesCoefficient[ Product[ComposeSeries[Series[Q[z], {z, 0, n}], Series[x[i] z, {z, 0, n}]], {i, 1, n}], n], Table[x[i], {i, 1, n}], Table[Subscript[c, i], {i, 1, n}]][[1]]] poly = K[Sqrt[#]/Tanh[Sqrt[#]] &, 4] /. c -> p; primeFactorForm[n_] := If[Length@# == 1, First@#, CenterDot @@ #] &[ Superscript @@@ FactorInteger[n]]; gcd = GCD @@ List @@ poly /. Rational[n_, d_]*c_ :> d; For[i = 0, i < 8, i++, poly = K[Sqrt[#]/Tanh[Sqrt[#]] &, i] /. c -> p; Print[Subscript[L, i], " = ", 1/primeFactorForm[gcd]* Plus @@ List @@ Distribute[gcd*poly] /. Times[Rational[n_, d_], e__] :> primeFactorForm[n]/ primeFactorForm[d]*e]] // Expand It outputs polynomials in different variables, factorizing everything and calculating the common denominator so it can be pulled out. I have some problems with formatting (I need this for a paper so it should look good). When the polynomial has many terms, the common denominator is out to the left and the rest is in a round bracket to the right (something like $\frac{1}{23}(2p_1+\frac{5p_2}{2})$, but with many more terms). But when there are just a few terms in the polynomial the output looks like this: $\frac{2p_1+\frac{5p_2}{2}}{23}$, which is quite ugly for a paper. Can someone tell me how to enforce it to use brackets all the time? Thank you!

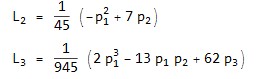
SimplifyorFactor? $\endgroup$For[i = 0, i < 8, i++, poly = K[Sqrt[#]/Tanh[Sqrt[#]] &, i] /. c -> p; Print[Subscript[L, i], " = ", ((1/gcd*Plus @@ List @@ Distribute[gcd*poly]) // Together) /. Times[Rational[n_, d_], e__] :> n/primeFactorForm[d]*e]]$\endgroup$