0
$\begingroup$

I have taken sequential partial derivatives of a two variable polynomial fraction, resulting in a very long series of polynomials of form:

C*x^i*y^j/(some product series of (1-x^k*y)^n)

What I wish to do is a series of basic truncations. First, I eliminate all polynomials that have x^i*y^j with i or j > 4 in the numerator. I keep looking over the documentation and StackExchange and cannot find anything that works for me.

I am open to suggestions.

Edit: Thus far, I have merely sorted the long series, and picked out the valid fractions starting from the bottom. What is the solution that uses Mathematica functions?

Improve this question
$\endgroup$
2
  • 1
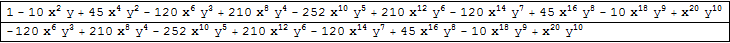
    $\begingroup$ Without a complete, even if simpler, example to work with, perhaps this is will work: Replace[expr, term_ /; MemberQ[Numerator[term], (x | y)^i_ /; i > 4] -> 0, 1]?? It assumes the expression for your rational function has been expanded in the way you describe. Please clarify whether this is right or wrong. $\endgroup$ Commented Jul 11, 2014 at 1:06
  • $\begingroup$ PolynomialReduce is a good function for this type of thing. $\endgroup$ Commented Jul 11, 2014 at 14:12

1 Answer 1

Reset to default
1
$\begingroup$

I post this as a way to handle polynomials that could be modified to suit your needs:

func[exp_, vars_, pattern_] := FromCoefficientRules[ Cases[CoefficientRules[exp, vars], HoldPattern[pattern]], vars]

Example:

expr = (1 - x^2 y)^10; Column[{Expand@expr, func[expr, {x, y}, Rule[{_?(# > 4 &), _}, _]]}, Frame -> All]

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.