To obtain derivatives of a numerical integral, one can try inactivating the integral, then differentiate, then activate. For example:
Inactive[NIntegrate][(x-ξ)^n f[ξ], {ξ, 0, x}]; D[%, x]
0^n f[x] + Inactive[NIntegrate][n (x - ξ)^(-1 + n) f[ξ], {ξ, 0, x}]
The problem with this approach is that in your application, $n<0$, and so differentiating this form of the integral is not useful. However, I again suggest that you transform the integration variable $\xi \to x - u$. Then:
Inactive[NIntegrate][u^n f[x-u], {u, 0, x}]; D[%, x]
x^n f[0] + Inactive[NIntegrate][u^n Derivative1[f][-u + x], {u, 0, x}]
This version doesn't suffer from fatal divide by 0 issues. We can package up the above ideas into a function:
RLDerivative[α_][f_] := With[{s = 1/Gamma[Ceiling[α]-α]}, RLFunction[ α, f, Function[{x,ϵ}, Evaluate @ D[ s Inactive[NIntegrate][u^(Ceiling[α]-α-1)f[x-u], {u, 0, ϵ I, x}], {x, Ceiling[α]} ] ] ] ] RLFunction[α_, f_, func_][x_?NumericQ] := Replace[ Quiet @ Check[Activate[func[x,0]], $Failed], $Failed :> (Message[RLFunction::ipath]; Activate[func[x, .1]]) ] RLFunction::ipath = "Unable to achieve convergence along the real axis. Integral path was deformed";
First note that I changed the path of integration to include $i \epsilon$. The default is to use $\epsilon =0$. However, there can be situations where the numerical integral doesn't converge. In that case, deforming the path of the integral can avoid this convergence issue. One down side is that using a complex path can introduce a spurious machine epsilon imaginary part. The other issue is the function under consideration may have a pole near $i \epsilon$ which will cause the deformed path integration to return an incorrect result.
Next, I split up the computation into two pieces. RLDerivative[α][f] will return an RLFunction object that can be applied to x values. This way the derivative of the inactive NIntegrate object only needs to be done once.
With those caveats mentioned, let's see how it works. First a test case that can be performed exactly:
int[n_, x_] = Integrate[(x-ξ)^n Exp[ξ], {ξ, 0, x}]; rlexp[α_, x_] := 1/Gamma[Ceiling[α]-α] D[int[Ceiling[α]-α-1, \[FormalX]], {\[FormalX], Ceiling[α]}]/. \[FormalX]->x
Now, compare RLDerivative with the exact rlexp:
rf = RLDerivative[.9][Exp]; rf /@ Range[5] rlexp[.9, Range[5]//N] rf = RLDerivative[12.2][Exp]; rf /@ Range[5] rlexp[12.2, Range[5]//N]
{2.75781, 7.40346, 20.0932, 54.603, 148.416}
{2.75781, 7.40346, 20.0932, 54.603, 148.416}
{1.12015*10^7, 2211.05, 34.6723, 55.0066, 148.438}
{1.12015*10^7, 2211.05, 34.6723, 55.0066, 148.438}
Now, for an example where the default integral path has convergence issues:
rf = RLDerivative[.9][Sin]; rf[.9]
RLFunction::ipath: Unable to achieve convergence along the real axis. Integral path was deformed
0.698049 + 2.99218*10^-14 I
Notice the warning message and the appearance of the small imaginary part resulting from the deformed path. Finally, the RLFunction looks like:
RLDerivative[1.9][Sin] (* RLFunction[1.9, Sin, Function[{x$, ϵ$}, 0.105114 (1/x$^0.9 + Inactive[NIntegrate][Sin[u - x$]/u^0.9, {u, 0, I ϵ$, x$}])]] *)
This looks a bit ugly, so here is a MakeBoxes rules for RLFunction, intended to mimic the standard M11 appearance of summary boxes for these types of functions:
RLFunction /: MakeBoxes[RLFunction[a_, f_, _], StandardForm] := RowBox[{ "FractionalDerivative","[", PanelBox[ RowBox[{ ToBoxes @ Plot[ f[x], {x,0,1}, Axes->False,Frame->True,FrameTicks->None, AspectRatio->1,ImageSize->20 ], "\" Order:\"", MakeBoxes[a,TraditionalForm] }], Background->GrayLevel[.95] ], "]" }]
Now, the RLFunction format hides the gory details:
RLDerivative[1.9][Sin]


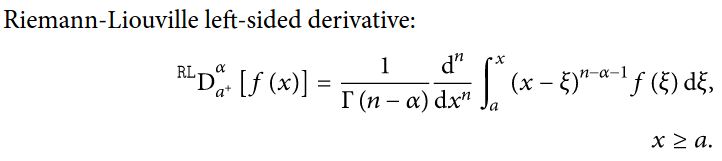
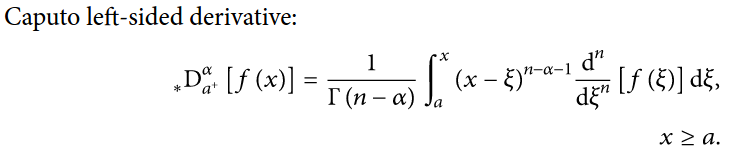

FractionalDandCaputoDare introduced in v13.1. $\endgroup$