10
$\begingroup$

Overview

I have a function that acts like the Interpolation on sparse $n$-dimensional data using a simple implementation of RBF interpolation method. I want my function to return a compiled function that will run fast. What I get works but it is much slower that I think it should be.

My code

Clear[RBFInterpolation] Options[RBFInterpolation] = { "DistanceFunction" -> (Norm[#1 - #2] &), "RadialBasisFunction" -> (Sqrt[#1^2 + #2^2/4] &), "RadialScale" -> Automatic, "Debug" -> False, "Compile" -> False}; RBFInterpolation[cptab_, opts : OptionsPattern[RBFInterpolation]] := Module[ {ro, xpts, fundata, Φ, disfun, λ, RBF, x}, xpts = #[[1]] & /@ cptab; fundata = #[[2]] & /@ cptab; disfun = OptionValue["DistanceFunction"]; RBF = OptionValue["RadialBasisFunction"]; Φ = Table[disfun[xpts[[i]], xpts[[j]]], {i, 1, Length[xpts]},{j,1,Length[xpts]}]; Which[ OptionValue["RadialScale"] == Automatic, ro = Median[ Flatten[Table[ Drop[Φ[[i]], {i}], {i, 1, Length[Φ]}]]], NumberQ[OptionValue["RadialScale"]], ro = OptionValue["RadialScale"], True, Print["I cannot understand \"RadialScale\"->", OptionValue["RadialScale"], " So I'm going to make it up"]; ro = Median[ Flatten[Table[ Drop[Φ[[i]], {i}], {i, 1, Length[Φ]}]]] ]; If[OptionValue["Debug"], Print["ro=", ro]]; If[OptionValue["Debug"], Print["Distance function on first two points"]; Print["point 1 ->", xpts[[1]]]; Print["point 2 ->", xpts[[2]]]; Print["Distance ->", disfun[xpts[[1]], xpts[[2]]]]; Print["Radial Basis Function on Distance ->", RBF[disfun[xpts[[1]], xpts[[2]]], ro]] ]; Φ = Map[RBF[#, ro] &, Φ, {2}]; If[OptionValue["Debug"], Print["Element of Φ[[1,1]]=", Φ[[1,1]]]]; λ = Inverse[Φ].fundata; If[OptionValue["Debug"], Print["First element of λ[[1]]=", λ[[i]]]]; If[OptionValue["Compile"], Return[ With[{xi = x, λi = λ, xptsi = xpts, roi = ro}, Compile[{{xi, _Real, 1}}, Sum[λi[[i]] RBF[disfun[xi, xptsi[[i]]], roi], {i, 1, Length[λ]}]]]], Return[ Function[x, Sum[λ[[i]] RBF[disfun[x, xpts[[i]]], ro], {i, 1, Length[λ]}]]] ] ];

Most of this function is not of interest to my question. I think the key is where I Return[] the compiled function.

Return[ With[{xi = x, λi = λ, xptsi = xpts, roi = ro}, Compile[{{xi, _Real, 1}}, Sum[λi[[i]] RBF[disfun[xi, xptsi[[i]]], roi], {i, 1, Length[λ]}]]]]

Testing the Function

The following code can be used to run and test the timing of the returned function.

First make a "Truth" function to sample then interpolate

Clear[truth] truth[x_] := Product[Sin[x[[i]]], {i, 1, Length[x]}];

Make up some data

n = 100; d = 5; cpts = RandomReal[{-π/2, π/2}, {n, d}]; cptab = {#, truth[#]} & /@ cpts; xpts = #[[1]] & /@ cptab; fundata = #[[2]] & /@ cptab;

Test the speed of the returned functions

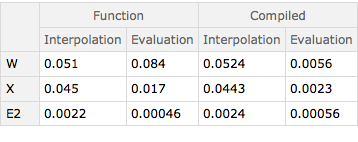
Print["Normal Function:"]; Timing[funFun = RBFInterpolation[cptab, "Compile" -> False];] Timing[funFun[#] & /@ xpts;] Print["Compile Function:"]; Timing[funFunc = RBFInterpolation[cptab, "Compile" -> True];] Timing[funFunc[#] & /@ xpts;] i = 1; Print["Normal function: ", funFun[xpts[[i]]]]; Print["Complie function: ", funFunc[xpts[[i]]]]; Print["The real right answer: ", fundata[[i]]];

I get results like this:

Normal Function: {0.080987,Null} {0.123981,Null} Compile Function: {0.092986,Null} {0.156977,Null} Normal function: -0.0182901 Complie function: -0.0182901 The real right answer: -0.0182901

So as you can see it works but it is not faster. How do I make this faster?

Simpler test that is faster!?

The code:

n = 10; a = RandomReal[{-1, 1}, n]; f = Table[2 π i, {i, 1, n}]; ϕ = RandomReal[{0, 2 π}, n]; Clear[Nfun] Nfun[t_] := Sum[a[[i]] Cos[f[[i]] t + ϕ[[i]]], {i, 1, n}]; Nfunc = Compile[{{t, _Real}}, Evaluate[Sum[a[[i]] Cos[f[[i]] t + ϕ[[i]]], {i, 1, n}]]]; Clear[makeNfunc] makeNfunc[a_, f_, ϕ_] := Module[{n}, n = Length[a]; Return[ Compile[{{t, _Real}}, Evaluate[Sum[a[[i]] Cos[f[[i]] t + ϕ[[i]]], {i, 1, n}]]]] ]; NfuncR = makeNfunc[a, f, ϕ];

Run the code:

npts = 10000; data = RandomReal[{0, 10}, npts]; Timing[Nfun[#] & /@ data;] Timing[Nfunc[#] & /@ data;] Timing[NfuncR[#] & /@ data;]

The output:

{0.585911, Null} {0.012998, Null} {0.012998, Null}

So in this simple case the compiled code is about 45 times faster for both the function compiled inline Nfunc and the function that was returned by the makeNfunc, NfuncR

So the question is what is the problem with my original function above?

Improve this question
$\endgroup$
5
  • $\begingroup$ I just want to add a link to an excellent package that provides a lot of $n$-space support Obtuse Package (I just need some more speed!) $\endgroup$ Commented Aug 29, 2013 at 22:45
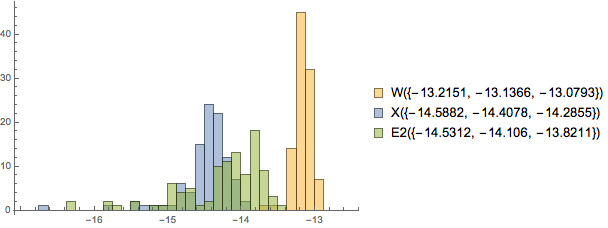
  • $\begingroup$ Compile has been improved since version 7, which I use, but when I run the line Timing[funFunc[#] & /@ xpts;] I get CompiledFunction::cfte: Compiled expression 0.` should be a rank 1 tensor of machine-size real numbers. >> CompiledFunction::cfex: Could not complete external evaluation at instruction 20; proceeding with uncompiled evaluation. >> Do you see similar errors? $\endgroup$ Commented Aug 30, 2013 at 0:59
  • $\begingroup$ In the code as shown in the post I do not get any errors. Early on I was playing with the rank which gave me similar errors. I then found that 1 worked which makes since because xi is a vector. I get no indication that what is returned is not compiled, like the error text proceeding with uncompiled evaluation. implies. If I just evaluate funFunc I get CompiledFunction[...stuff..] as expected. Everything works it is just no faster. $\endgroup$ Commented Aug 30, 2013 at 1:13
  • $\begingroup$ I added an answer. If I am correct using CompilationOptions -> {"InlineExternalDefinitions" -> True} will fix your problem. $\endgroup$ Commented Aug 30, 2013 at 1:18
  • $\begingroup$ The routine given here for thin plate splines might be useful to you; you will only need to change the underlying RBF. $\endgroup$ Commented Jul 25, 2015 at 14:36

3 Answers 3

Reset to default
10
$\begingroup$

I had to modify your code to get it to work without error in version 7. Once I did it that appears to be working correctly and faster than the non-compiled code.

I needed to inject the values of RBF and disfun into the Compile using With:

With[{iRBF = RBF, idisfun = disfun}, If[OptionValue["Compile"], Return[With[{xi = x, λi = λ, xptsi = xpts, roi = ro}, Compile[{{xi, _Real, 1}}, Sum[λi[[i]] iRBF[idisfun[xi, xptsi[[i]]], roi], {i, 1, Length[λ]}]]]], Return[Function[x, Sum[λ[[i]] iRBF[idisfun[x, xpts[[i]]], ro], {i, 1, Length[λ]}]]]] ]

I believe that in later versions this can be done with:

CompilationOptions -> {"InlineExternalDefinitions" -> True}

Now running your test:

n = 300; d = 5; cpts = RandomReal[{-\[Pi]/2, \[Pi]/2}, {n, d}]; cptab = {#, truth[#]} & /@ cpts; xpts = #[[1]] & /@ cptab; fundata = #[[2]] & /@ cptab; Print["Normal Function:"]; Timing[funFun = RBFInterpolation[cptab, "Compile" -> False];] Timing[funFun /@ xpts;] Print["Compile Function:"]; Timing[funFunc = RBFInterpolation[cptab, "Compile" -> True];] Timing[funFunc /@ xpts;] i = 1; Print["Normal function: ", funFun[xpts[[i]]]]; Print["Complie function: ", funFunc[xpts[[i]]]]; Print["The real right answer: ", fundata[[i]]];

Normal Function:

{0.514, Null}

{0.546, Null}

Compile Function:

{0.515, Null}

{0.094, Null}

Normal function: 0.000268092

Complie function: 0.000268092

The real right answer: 0.000268092

Improve this answer
$\endgroup$
6
  • $\begingroup$ Thank you I had tried many combos with With but I missed that one thank you. $\endgroup$ Commented Aug 30, 2013 at 1:20
  • $\begingroup$ @c186282 You're welcome, and thanks for the Accept. However, I recommend waiting 24 hours to give everyone around the world a chance to answer. People may have even better ways to speed your code, if you give them a chance. $\endgroup$ Commented Aug 30, 2013 at 1:22
  • $\begingroup$ Thank you for the advice I will toggle the answer for 24 hours. Also thank you for the edit. How did you turn \Pi in the real symbol? $\endgroup$ Commented Aug 30, 2013 at 1:25
  • $\begingroup$ @c186282 One of your users provided a wonderful browser script that adds a button to the editor for that. Also see (1137). $\endgroup$ Commented Aug 30, 2013 at 1:48
  • $\begingroup$ OK it has been 24 hours $\endgroup$ Commented Aug 31, 2013 at 0:27
6
$\begingroup$

The following is somewhat faster. The principal changes are:

  • The use of a distance function Sqrt@Total[(#1-Transpose@#2)^2]& that computes an array of distances for disfun[x, {y1, y2,...}] that is much faster than mapping Norm over individual pairs.

  • The use of Dot instead of Sum. Dot is much faster. In fact, the uncompiled function, which is fully vectorized, is sometimes faster than the compiled function.

  • The vectorized use of RBF to compute the final Φ, following @xzczd's example.

  • The use of LinearSolve instead of Inverse, which is both faster and more numerically stable. (The maximum relative difference in the solutions was about 10^-13 to 10^-12 on a few random examples.)

Since not all distance functions and RBFs can be vectorized, some tests were added to switch to the slower point-by-point methods when the faster methods are not possible.

Clear[RBFInterpolationE2] Options[RBFInterpolationE2] = { "DistanceFunction" -> Automatic,(*(Sqrt@Total[(#1-Transpose@#2)^2]&)=Norm[x1,#]&/@x2*) "RadialBasisFunction" -> (Sqrt[#1^2 + #2^2/4] &), "RadialScale" -> Automatic, "Debug" -> False, "Compile" -> False}; RBFInterpolationE2[cptab_, opts : OptionsPattern[]] := Module[{ro, xpts, fundata, Φ, disfun, λ, RBF, x, dfThreadableQ, rbfListableQ, body}, xpts = #[[1]] & /@ cptab; fundata = #[[2]] & /@ cptab; disfun = OptionValue["DistanceFunction"]; If[disfun === Automatic, disfun = Sqrt@Total[(#1 - Transpose@#2)^2] &; (* vectorized & "threadable" norm *) dfThreadableQ = True, dfThreadableQ = False (* could add options or heuristics *) ]; RBF = OptionValue["RadialBasisFunction"]; rbfListableQ = ListQ[RBF[{0.}, 1.]]; If[dfThreadableQ, (*Φ=DistanceMatrix[xpts] (* not faster for the default distance *)*) Φ = disfun[#, xpts] & /@ xpts, Φ = Table[disfun[xpts[[i]], xpts(*[[j]]*)], {i, 1, Length[xpts]}, {j, 1, Length[xpts]}] ]; Which[ OptionValue["RadialScale"] == Automatic , ro = Median[Flatten[Table[Drop[Φ[[i]], {i}], {i, 1, Length[Φ]}]]], NumberQ[OptionValue["RadialScale"]] , ro = OptionValue["RadialScale"], True , Print["I cannot understand \"RadialScale\"->", OptionValue["RadialScale"], " So I'm going to make it up"] ; ro = Median[Flatten[Table[Drop[Φ[[i]], {i}], {i, 1, Length[Φ]}]]] ]; If[rbfListableQ, Φ = RBF[Φ, ro], (*xzczd; assumes RBF is Listable *) Φ = Map[RBF[#, ro] &, Φ, {2}] ]; λ = LinearSolve[Φ, fundata]; (* was λ=Inverse[Φ].fundata *) With[{λi = λ, xptsi = xpts, roi = ro, RBFi = RBF, disfuni = disfun}, If[dfThreadableQ, (* construct code for the interpolating function *) body = Hold[x, Dot[λi, RBFi[disfuni[x, xptsi], roi]]], body = Hold[x, Dot[λi, RBFi[disfuni[x, #] & /@ xptsi], roi]] ]; If[OptionValue["Compile"], Return[body /. Hold[x_, code_] :> Compile[{{x, _Real, 1}}, code, RuntimeAttributes -> {Listable}, Parallelization -> True]], Return[body /. Hold[x_, code_] :> Function[x, code]] ]] ];

The following shows the timings of Mr.Wizards (W), xzczd's (X) and my (E2) codes.

ClearAll[run]; run[meth_String] := Module[{ans, funFun}, With[{RBFI = ToExpression["RBFInterpolation" <> meth]}, <| "Function" -> <| "Interpolation" -> First@RepeatedTiming[funFun = RBFI[cptab, "Compile" -> False]], "Evaluation" -> First@RepeatedTiming[ans = funFun /@ xpts], "RBFI" -> funFun, "Values" -> ans |>, "Compiled" -> <| "Interpolation" -> First@RepeatedTiming[funFun = RBFI[cptab, "Compile" -> True]], "Evaluation" -> First@RepeatedTiming[ans = funFun /@ xpts], "RBFI" -> funFun, "Values" -> ans |> |> ]]; ds = Dataset[AssociationMap[run, {"W", "X", "E2"}]]; (* kinda roundabout transposing, maybe *) Transpose[ds[[All, All, {"Interpolation", "Evaluation"}]]][[All, All, All]] // Transpose

Mathematica graphics

The parallelization of the compiled function is not used in the above timings. If we use parallelization (by calling the compiled function on all points at once), the compiled function beats the uncompiled one (Mac, Intel i7, 4(8) cores):

funFun = ds["E2", "Compiled", "RBFI"]; First@RepeatedTiming[funFun@xpts] (* 0.00014 *)

The OP compares the three methods with the OP's original code at points between the interpolation points. All three methods do pretty well at these points.

With[{errdata = Reap[Query[All, "Compiled", Sow@RealExponent[#Values - fundata] &]@ds][[2, 1]]}, Histogram[ MapThread[Legended[#, #2@Quartiles[#]] &, {errdata, Normal@Keys[ds]}], {1./8}, PlotRange -> {{-17, -12.5}, All}] ]

Mathematica graphics

The following compares the three methods with the OP's original code at points between the interpolation points. Mr.Wizard s code produces results that are exactly equal to the OP's. There's a small but significant error in xzczd's results, which I do not have time to explore. The error in my results are consistent with the differences in the code, such as LinearSolve instead of Inverse (the condition number of the matrix Φ is around 10^5 or so on the random point sets cptab I checked).

funFun = RBFInterpolation[cptab, "Compile" -> True]; valsOP = funFun /@ MovingAverage[xpts, 2]; cfs = Query[All, "Compiled", "RBFI"]@ds // Normal // Values; errdata2 = (Transpose[Through[cfs[#]] & /@ MovingAverage[xpts, 2] - valsOP]); Grid@Transpose@{Normal@Keys[ds], Quartiles /@ RealExponent@errdata2}

Mathematica graphics

Improve this answer
$\endgroup$
4
$\begingroup$

You code can be even faster. The main idea is to make use of vecterization as much as possible:

Clear[RBFInterpolation] Options[RBFInterpolation] = {"DistanceFunction" -> (Norm[#1 - #2] &), "RadialBasisFunction" -> (Sqrt[#1^2 + #2^2/4] &), "RadialScale" -> Automatic, "Debug" -> False, "Compile" -> False}; RBFInterpolation[cptab_, opts : OptionsPattern[RBFInterpolation]] := Module[{ro, xpts, fundata, Φ, disfun, λ, RBF, x}, (* Modification 1 *) xpts = cptab\[Transpose][[1]]; fundata = cptab\[Transpose][[2]]; disfun = OptionValue["DistanceFunction"]; RBF = OptionValue["RadialBasisFunction"]; (* Modification 2 *) Φ = Outer[disfun, xpts, xpts, 1]; Which[OptionValue["RadialScale"] == Automatic, (* Modification 3, but this seems not to speed up much *) ro = With[{l = Length@Φ}, Sort[Flatten[Φ][[l + 1 ;;]]][[Ceiling[l/2]]]], NumberQ[OptionValue["RadialScale"]], ro = OptionValue["RadialScale"], True, Print["I cannot understand \"RadialScale\"->", OptionValue["RadialScale"], " So I'm going to make it up"]; ro = With[{l = Length@Φ}, Sort[Flatten[Φ][[l + 1 ;;]]][[Ceiling[l/2]]]]]; If[OptionValue["Debug"], Print["ro=", ro]]; If[OptionValue["Debug"], Print["Distance function on first two points"]; Print["point 1 ->", xpts[[1]]]; Print["point 2 ->", xpts[[2]]]; Print["Distance ->", disfun[xpts[[1]], xpts[[2]]]]; Print["Radial Basis Function on Distance ->", RBF[disfun[xpts[[1]], xpts[[2]]], ro]]]; (* Modification 4 *) Φ = RBF[Φ, ro]; If[OptionValue["Debug"], Print["Element of Φ[[1,1]]=", Φ[[1, 1]]]]; λ = Inverse[Φ].fundata; If[OptionValue["Debug"], Print["First element of λ[[1]]=", λ[[i]]]]; (* Modification 5 *) With[{iRBF = RBF, idisfun = disfun}, If[OptionValue["Compile"], With[{xi = x, λi = λ, xptsi = xpts, roi = ro}, Compile[{{xi, _Real, 1}}, Total[λi iRBF[idisfun[xi, #] & /@ xptsi, roi]]]], Function[x, Total[λ iRBF[idisfun[x, #] & /@ xpts, ro]]]]]];

Notice that Modification 4 and 5 requires "RadialBasisFunction" to be Listable, which is true for most arithmetic function. You may want to add some protective code (or use Map instead if you don't want to take the risk) in these parts.

Let's try your test:

Clear[truth] truth[x_] := Product[Sin[x[[i]]], {i, 1, Length[x]}]; n = 300; d = 5; cpts = RandomReal[{-π/2, π/2}, {n, d}]; cptab = {#, truth[#]} & /@ cpts; xpts = #[[1]] & /@ cptab; fundata = #[[2]] & /@ cptab; Print["Normal Function:"]; Timing[funFun = RBFInterpolation[cptab, "Compile" -> False];] Timing[funFun /@ xpts;] Print["Compile Function:"]; Timing[funFunc = RBFInterpolation[cptab, "Compile" -> True];] Timing[funFunc /@ xpts;] i = 1; Print["Normal function: ", funFun[xpts[[i]]]]; Print["Complie function: ", funFunc[xpts[[i]]]]; Print["The real right answer: ", fundata[[i]]];

enter image description here

For comparison, the following is the timing of Mr.Wizard's code on my machine:

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.