19
$\begingroup$

Now I am trying to fit some data with a implicit model function.

Firstly, I tried a toy example.

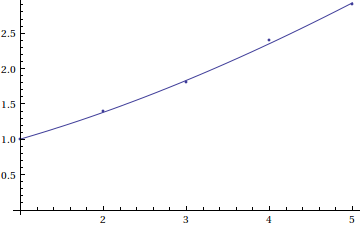
Toy example with input and output

data = {{1, 1}, {2, 1.4}, {3, 1.8}, {4, 2.4}, {5, 2.9}}; fitfunc[a_,b_,x_] := y /. FindRoot[a y + b Log[y] == x, {y, 1}]; FindFit[data, fitfunc[a, b, x], {a, b}, x]

Mathematica gives the following warning message and answer:

FindRoot::nlnum: The function value {0. +1. a-1. x} is not a list of numbers with dimensions {1} at {y} = {1.}. >>
ReplaceAll::reps: {FindRoot[a y+b Log[y]==x,{y,1}]} is neither a list of replacement rules nor a valid dispatch table, and so cannot be used for replacing. >>
{a -> 0.986636, b -> 1.96879}

The fit seems good.

Show[ListPlot[data], ContourPlot[Evaluate[a y + b Log[y] == x /. %], {x, 1, 5}, {y, 1, 4}]]

The fit result:

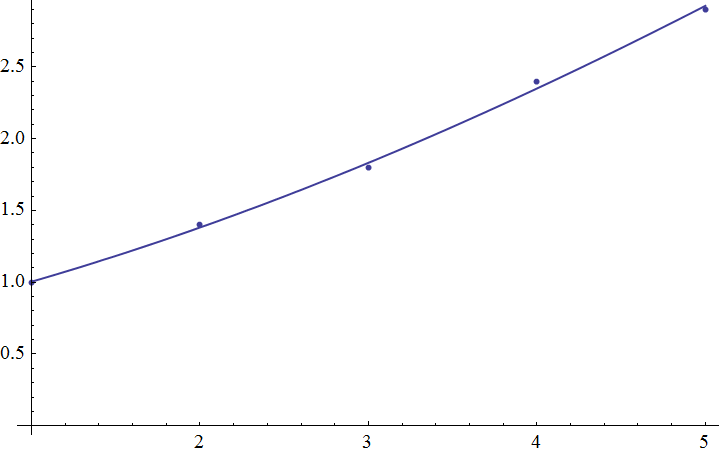
enter image description here

I have read the documentation of Symbolic Evaluation, and tried to use NumberQ in the function declaration, but I got the same warning message.

What am I doing wrong and how to solve this problem to avoid the warning message?

Improve this question
$\endgroup$
0

3 Answers 3

Reset to default
15
$\begingroup$

One can always fall back on the definition of least-squares fitting, if the situation demands:

data = {{1, 1}, {2, 1.4}, {3, 1.8}, {4, 2.4}, {5, 2.9}}; {a, b} = NArgMin[Norm[Function[{x, y}, \[FormalA] y + \[FormalB] Log[y] - x] @@@ data], {\[FormalA], \[FormalB]}] {0.9909829665303092, 1.952060702019563} Show[ListPlot[data], ContourPlot[a y + b Log[y] == x, {x, 1, 5}, {y, 1, 4}]]

fit of implicit nonlinear model

Note the use of formal parameters as stand-ins for the parameters sought within NArgMin[].

Improve this answer
$\endgroup$
5
  • $\begingroup$ Note, also, that this version returns a lower value for the least squares objective function (0.129153) as opposed to the version using FindFit[]+FindRoot[] (0.129416). $\endgroup$ Commented Aug 31, 2012 at 12:19
  • 6
    $\begingroup$ +1 This answer is squarely within the spirit of the question: if the function is to be defined implicitly, then we are not emphasizing errors in either the x or y directions (unlike FindFit), but should be penalizing them in a symmetric way, which is what this approach does. $\endgroup$ Commented Aug 31, 2012 at 13:21
  • $\begingroup$ A 2 per mil in the objective function ... OMG $\endgroup$ Commented Aug 31, 2012 at 13:58
  • $\begingroup$ @belisarius, if you're angling for four good digits... :) $\endgroup$ Commented Aug 31, 2012 at 14:03
  • $\begingroup$ JM: Help yourself and remove some data points :) $\endgroup$ Commented Aug 31, 2012 at 14:31
14
$\begingroup$

It's an evaluation problem. fitfunc[a, b, x] evaluates to your definition which is y /. FindRoot[a y + b Log[y] == x, {y, 1.}] this returns the error, since it cannot find the root without numeric arguments for a and b. To avoid it, you need to tell it not to evaluate your function until you have numeric arguments. I assume this is what you tried to do with NumberQ.

 data = {{1, 1}, {2, 1.4}, {3, 1.8}, {4, 2.4}, {5, 2.9}}; fitfunc[a_?NumericQ, b_?NumericQ, x_?NumericQ] := y /. FindRoot[a y + b Log[y] == x, {y, 1.}]; FindFit[data, fitfunc[a, b, x], {a, b}, x]

Returns

{a -> 0.986636, b -> 1.96879}

With no warning messages

Improve this answer
$\endgroup$
2
  • $\begingroup$ Thanks very much! It works well now. $\endgroup$ Commented Aug 31, 2012 at 11:43
  • 5
    $\begingroup$ Of course, in this toy example, explicit solution is also available. $y = \frac{b}{a} W\left(\frac{a}{b}\exp\left(\frac{x}{b}\right)\right)$. Using fitfuncExact[a_, b_, x_] := ProductLog[a/b Exp[x/b]] b/a gives the same fitted parameters. $\endgroup$ Commented Aug 31, 2012 at 12:48
12
$\begingroup$ 
data = {{1, 1}, {2, 1.4}, {3, 1.8}, {4, 2.4}, {5, 2.9}}; fitfunc[a_, b_, x_] := y /. Solve[a y + b Log[y] == x, {y},InverseFunctions -> True]; FindFit[data, fitfunc[a, b, x], {a, b}, x]

When inverse functions are allowed, Solve solves for f[expr] first, then applies InverseFunction[f] to the result, equates it to expr, and continues trying to solve for the remainder of the variables.

Improve this answer
$\endgroup$
1
  • $\begingroup$ This provides another method to fit a implicit function. I appreciate your nice answer. $\endgroup$ Commented Aug 31, 2012 at 11:49

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.