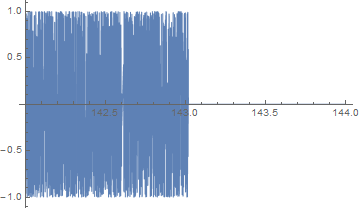
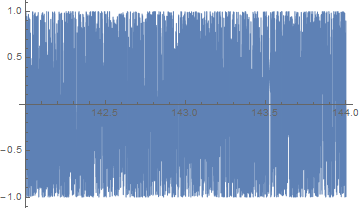
When plotting the graph of $\sin(x^x)$ I noticed that there is no plot from about $x=143$. I don't suppose there is a purely mathematical explanation for this?
So, why is there no graph in Mathematica from $x=143$? Some kind of overflow?
f[x_] = Sin[x^x] Plot[{f[x]}, {x, 142, 144}, PlotStyle -> Thin, PlotLegends -> "Expressions"] 
Normally Plot uses machine precision numbers; your $x^x$ expression is hitting the limit of the numbers that can be represented in machine precision right about $x>143$.
Note:
Solve[$MaxMachineNumber == x^x, x] (* Out: {{x -> 143.016}} *) You can increase the WorkingPrecision setting for Plot adequately, and the plot will be complete:
f[x_] = Sin[x^x] Plot[{f[x]}, {x, 142, 144}, PlotStyle -> Thin, PlotLegends -> "Expressions", WorkingPrecision -> 450] 
