1
$\begingroup$

I have data points — denoted by Fk— covering quite a large range $(1,\,10^{1010})$. I plotted them with ListLogPlot. Then I tried to fit the data points using NonlinearModelFit, and now I have two problems:

  1. Fitting the data points

    fit = NonlinearModelFit[Fk[300], a*k^(B*k), {a, B}, k]

    gives 1 k^1 for the fitted model.

    However, fitting the data points with: 

    fit2 = NonlinearModelFit[Fk[300], a*k^(b*c*k), {a, b, c}, k]

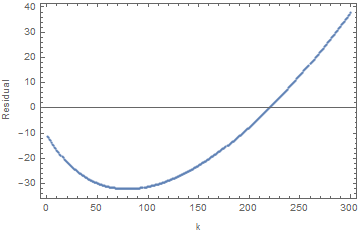
    gives the fitted model 140.714 k^1.16997 k which I completely do not unterstand. I mean why should the output change upon inserting the variable $c$, which could also be combined with $b$ such that say $b\,c= B$ and fit should be equal to fit2.

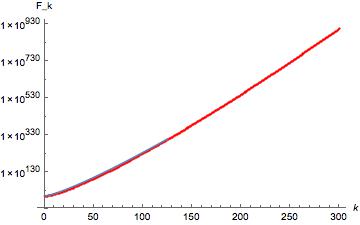
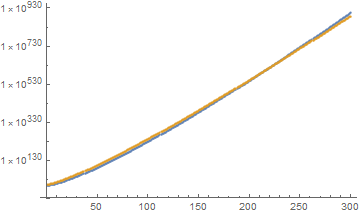
  2. If I now plot the data Fk vs. k together with the fitted model, the fitted curve ends at some value of $k \approx 120$, and I do not unterstand why. My code for this is

    Show[{ListLogPlot[Fk[300], PlotStyle -> Red], LogPlot[fit2[k], {k, 0, 300}]}]

plot

Red dots = data points; blue line = fitted curve

Improve this question
$\endgroup$
10
  • $\begingroup$ Thanks, is it now ok? $\endgroup$ Commented Feb 26, 2017 at 13:03
  • $\begingroup$ Yes, I will delete my comment. $\endgroup$ Commented Feb 26, 2017 at 13:05
  • $\begingroup$ Can you provide us with your points? (Btw it makes no sense to fit b*c since they're directly correlated into each other.) $\endgroup$ Commented Feb 26, 2017 at 14:13
  • $\begingroup$ For the fact that the plot stops at a value around k=120, that may be because your function is hitting the upper limit of machine-precision numbers. See (105774). Try increasing the WorkingPrecision for your Plot function. $\endgroup$ Commented Feb 26, 2017 at 15:49
  • $\begingroup$ Non-linear fitting rarely plug-and-play. Two things I would recommend: (i) Find a good initial guess for the parameters. E.g., a=Fk[0]. (ii) If the fit is 1% off at k=300 the absolute error is $10^{800}$ times larger than a 1000% error at k=50. That is, you probably want to specify weights to be some function of Fk. Finally, plotting works with Exclusions -> None, see this bug. $\endgroup$ Commented Feb 26, 2017 at 16:20

1 Answer 1

Reset to default
4
$\begingroup$

You want to fit the log of Fk[300] and add in some constraints for the parameters.

Fk[n_] := LinearSolve[ Table[PadRight[Table[StirlingS2[k, m], {m, k}], n], {k, 1, n}], Table[BellB[k]^2, {k, 1, n}]]; data = Transpose[{Range[1, 300], Log[Fk[300]]}]; nlm = NonlinearModelFit[data, {Log[a] + b k Log[k], a > 0 && b > 0}, {a, b}, k]; nlm["BestFitParameters"] (* {a -> 74145.49180618675`,b -> 1.1879871492270795`} *)

But this doesn't provide a great fit. (Or rather if you add in a few more terms, you can predict a whole lot better. But that's not a Mathematica issue.)

ListLogPlot[{Fk[300], Exp[nlm["PredictedResponse"]]}]

Fit using logs

Here is a "close-up" of the lack of fit showing the residual associated with the values of k: Residuals vs k

Improve this answer
$\endgroup$
4
  • $\begingroup$ Hi Jim. Thanks for your answer. I now used your NonlinearModelFit however I got a different a and b: {a -> 1.70003*10^-6, b -> 1.20435} $\endgroup$ Commented Feb 27, 2017 at 7:03
  • $\begingroup$ And yes, you are right it is not the best fit. I will try to make it better, but what I am looking for is just an asymptotic behaviour of the Fk, thus from the fit I already kind of see what to expect. $\endgroup$ Commented Feb 27, 2017 at 7:13
  • $\begingroup$ Using loga as the parameter rather than a in Log[a] gives a number much closer to yours and (maybe more importantly) gives a smaller error variance. However, if your objective is to estimate asymptotic behaviour and you're not so interested in small values of k, then that probably doesn't help much. $\endgroup$ Commented Feb 27, 2017 at 17:06
  • $\begingroup$ Yeah I realized that even for getting just an asymptotic behaviour my fit was far too bad, thus I changed the model to ak^(bk^c). Now the fit is much better and the residuals pretty small. Thanks again for your answer. $\endgroup$ Commented Feb 28, 2017 at 7:04

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.