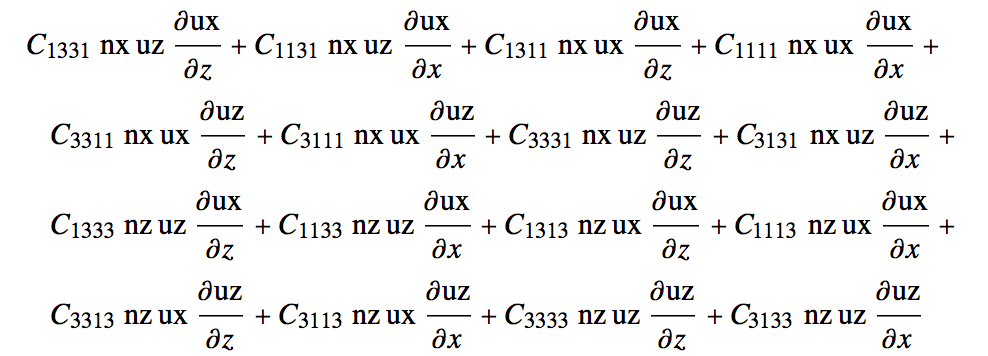2
$\begingroup$

I am quite new in Mathematica (1 week new) and after many trials I did not manage to make my partial derivatives to look traditional way.

There are few topics such as How to make traditional output for derivatives and Customizing display of partial differential equations answering this question, but in my case all proposed methods does not give desirable result.

Want this: $\frac{\partial u_x}{\partial x} + \frac{\partial u_x}{\partial z} + \frac{\partial u_z}{\partial x} + \frac{\partial u_z}{\partial z}$

Have this: $u_x^{(0,0,1)}(x,0,z) + ...$ or $\frac{\partial uv[[1]]} {\partial xz[[1]]}+...$

I would like to expand equation $n_l u_k C_{ijkl} u_{i,j}$. For this purpose I am doing sum over all 4 $ijkl$ indices and result looks as I want but partial derivatives

Code that I am using:

nv = {nx, 0, nz}; uv = {ux[x, 0, z], 0, uz[x, 0, z]}; xz = {x, 0, z}; CC = Array[C_{ToExpression@StringJoin@IntegerString@ {#1, #2, #3, #4}} &, {3, 3, 3, 3}]; (* _{ToExpression@StringJoin@IntegerString@ {#1, #2, #3, #4}} stands for a subscript of C *) ux /: Format[ux[___]] := ux; uz /: Format[uz[___]] := uz; TraditionalForm[Sum[Part[nv, l] Part[uv, k] Part[CC, i, j, k, l] D[Part[uv, i], Part[xz, j]], {i, {1, 3}}, {j, {1, 3}}, {k, {1, 3}}, {l, {1, 3}}]]

If you have any ideas I am grateful in advance

Thanks!

Improve this question
$\endgroup$
2
  • $\begingroup$ Welcome to Mathematica.SE! 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Take the tour and check the help center! 3) When you see good questions and answers, vote them up by clicking the vote triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! $\endgroup$ Commented Jun 28, 2016 at 14:36
  • $\begingroup$ Have you seen this? mathematica.stackexchange.com/questions/23659/… $\endgroup$ Commented Jun 28, 2016 at 15:09

1 Answer 1

Reset to default
3
$\begingroup$

I've edited my answer in the linked thread so that it can now be used without modification. Previously, you had to define the functions uv that you wish to differentiate in a more general way, replacing the explicit 0 in their argument with y. The reason is that my earlier answer assumed differentiations are performed on the given function, not on the new function obtained by setting one function argument equal to a constant.

However, now it works with the unchanged definitions in the question (except that I corrected a formatting error in your CC):

nv = {nx, 0, nz}; uv = {ux[x, 0, z], 0, uz[x, 0, z]}; xz = {x, 0, z}; CC = Array[ Subscript[C, ToExpression@StringJoin@IntegerString@{#1, #2, #3, #4}] &, {3, 3, 3, 3}]; ux /: Format[ux[___]] := ux; uz /: Format[uz[___]] := uz; TraditionalForm[ Sum[Part[nv, l] Part[uv, k] Part[CC, i, j, k, l] D[Part[uv, i], Part[xz, j]], {i, {1, 3}}, {j, {1, 3}}, {k, {1, 3}}, {l, {1, 3}}]]

output 2

Improve this answer
$\endgroup$
0

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.