6
$\begingroup$

I have a point cloud as X,Y,Z-coordinates which form a parallelepiped (with most data points inside the solid) that is rotated in space by some unknown amount and would like to find the 8 corners of it.

Basically, the answer could just be (using data.csv)

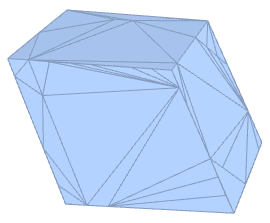
CFF[v_] := (v/{255, -255, 512})[[{3, 1, 2}]]; pts = CFF /@ Import["data.csv"]; H = ConvexHullMesh@pts corners = MeshCoordinates@H

However, the mesh found by ConvexHullMesh looks like this:

Convex Hull

As you can see, there are a number of extra mesh points that are not inside but exactly on the 6 faces, so they get treated as belonging the convex hull.

How can I simplify the mesh, ie. remove coplanar points?

Thank you for any suggestions.

I have tried TriangulateMesh, but get a very unhelpful "TriangulateMesh failed to triangulate the mesh." DiscretizeRegion crashes the kernel in 11 and fails with "DiscretizeRegion was unable to discretize the region" in 10.

Improve this question
$\endgroup$
7
  • $\begingroup$ TriangulateMesh[%, MaxCellMeasure -> \[Infinity]]? $\endgroup$ Commented Jan 19, 2017 at 14:34
  • $\begingroup$ @Feyre: tried that, "TriangulateMesh failed to triangulate the mesh." Also, DiscretizeRegion crashes the kernel. Added to question, sorry about that. $\endgroup$ Commented Jan 19, 2017 at 14:43
  • 1
    $\begingroup$ Helping you would be easier if you could post the "point cloud as X,Y,Z-coordinates which form a parallelepiped", here or in Pastebin if it's too long. $\endgroup$ Commented Jan 19, 2017 at 14:52
  • $\begingroup$ I have added a slightly decimated dataset that has the same issues. The reshaping is neccessary for the full processing, leaving it in because the type of the numbers might matter. $\endgroup$ Commented Jan 19, 2017 at 15:11
  • 1
    $\begingroup$ Region`Mesh`MergeCells may be of use per this answer $\endgroup$ Commented Feb 4, 2021 at 8:55

1 Answer 1

Reset to default
4
$\begingroup$

We can find all the corners thusly:

i = Flatten@{Position[a = pts[[All, #]], Min@a] & /@ Range[3], Position[a = pts[[All, #]], Max@a] & /@ Range[3]}; corners = pts[[#]] & /@ i

{{0, 0, 0}, {359/512, -(256/255), -(89/255)}, {15/ 128, -(43/255), -(262/255)}, {1, 0, 0}, {153/512, 256/255, 89/ 255}, {113/128, 43/255, 263/255}}

Show[H, ListPointPlot3D[corners, PlotStyle -> {Red, PointSize[0.1]}]]

enter image description here

We can finish the set with:

corners = Join[corners, {corners[[3]] + corners[[5]], corners[[3]] + corners[[6]], corners[[2]] - corners[[3]]}]

{{0, 0, 0}, {359/512, -(256/255), -(89/255)}, {15/ 128, -(43/255), -(262/255)}, {1, 0, 0}, {153/512, 256/255, 89/ 255}, {113/128, 43/255, 263/255}, {213/512, 71/85, -(173/255)}, {1, 0, 1/255}, {299/512, -(71/85), 173/255}}

ConvexHullMesh@corners

enter image description here

Improve this answer
$\endgroup$
2
  • $\begingroup$ That does indeed solve this particular application, but I do wonder if there isn't a way to do this using the geometric functions... $\endgroup$ Commented Jan 19, 2017 at 19:25
  • $\begingroup$ @Martok Like you said TriangulateMesh[] fails, that would be the go-to build in function to do this. $\endgroup$ Commented Jan 19, 2017 at 19:43

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.