6
$\begingroup$

We have a built-in function Nearest which returns a function for evaluating the nearest value of inputs. However, as a slight variant, I would like to construct a "function object" created from a one-dimensional data $\{x_i\}$ that finds the largest value $x_i < x$ for a given input $x$.

I suspect that Nearest might be designed to handle high-dimensional data where the ordering of two points are not well-defined so the underlying data structures might differ for my purpose.

I can manually make this type of function by sorting the data initially and calculating results through a binary search. But I think this type of problem is prevalent so probably there might be an elegant (or built-in) way of solving this problem.

Improve this question
$\endgroup$
1
  • 3
    $\begingroup$ You should still be able to use Nearest[] for this, if you change DistanceFunction accordingly. Alternatively, there's the (undocumented) function GeometricFunctions`BinarySearch[]. $\endgroup$ Commented Jan 31, 2017 at 12:14

5 Answers 5

Reset to default
7
$\begingroup$

One can use Interpolation with InterpolationOrder -> 0:

SeedRandom[1]; data = RandomReal[1, 10] (* {0.817389, 0.11142, 0.789526, 0.187803, 0.241361, 0.0657388, 0.542247, 0.231155, 0.396006, 0.700474} *) nf = Evaluate@ Interpolation[Transpose@{-data, data}, InterpolationOrder -> 0, "ExtrapolationHandler" -> {With[{m = -Max[data]}, Piecewise[{{-m, # < m}}, Indeterminate] &], "WarningMessage" -> False} ][-#] &; Plot[nf[x], {x, -0.5, 1.5}, Epilog -> {Red, PointSize@Medium, Point[Transpose@{data, data}]}]

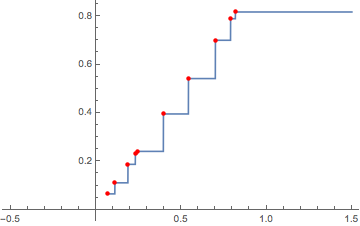
Mathematica graphics

Replace Indeterminate with the value desired when the input falls below the minimum of the data.

Interpolation[] takes longer than Nearest[] to form the function, but it is faster to evaluate on large data:

SeedRandom[1]; data = RandomReal[1, 1000000]; nf = Evaluate@ Interpolation[Transpose@{-data, data}, InterpolationOrder -> 0, "ExtrapolationHandler" -> {With[{m = -Max[data]}, Piecewise[{{-m, # < m}}, Indeterminate] &], "WarningMessage" -> False} ][-#] &; // RepeatedTiming nf /@ RandomReal[1, 1000]; // RepeatedTiming (* {1.43, Null} {0.0043, Null} *) (* Sascha's distance function dist[] *) nf2 = Nearest[data, DistanceFunction -> dist]; // RepeatedTiming nf2 /@ RandomReal[1, 2]; // RepeatedTiming (* {0.000015, Null} {4.4, Null} *)

Relative speed vs. length of data to evaluate the function on an input, showing that nf becomes orders of magnitude faster as the size of data increases:

Length@data 1000 10000 100000 1000000 nf2/nf 700 7000 60000 600000

The speed to form nf2 stays roughly constant. The speed to form nf is roughly linear.
The speed of nf2 seems to be improved by pre-sorting data by about 10-15%; sorting for n = 1000000 takes about 0.16 sec. on my machine.

Improve this answer
$\endgroup$
2
  • $\begingroup$ You will get a little bit of speed up if you do: nf[data] instead of nf /@ data. $\endgroup$ Commented Jan 31, 2017 at 23:34
  • $\begingroup$ @CarlWoll Thanks. I forgot I knew that. :) OTOH, whether that is a fair comparison depends on the use-case, I suppose. $\endgroup$ Commented Jan 31, 2017 at 23:37
6
$\begingroup$

You can use DistanceFunction as in

dist[u_, x_] := 1000000 (* some big number *) /; x > u dist[u_, x_] := Abs[u - x]

and use it like

Nearest[{1, 2, 2.9, 3, 4} , 2.99, DistanceFunction -> dist] (* 2.9 *)

Unfortunately using Infinity in the first Definition of dist does yield an error

Nearest::nearuf: The user-supplied distance function dist does not give a real numeric distance when applied to the point pair 2.99` and 3.

so you have to supply an appropriately big number instead.

Improve this answer
$\endgroup$
1
  • 2
    $\begingroup$ $MaxNumber or $MaxMachineNumber? (+1) $\endgroup$ Commented Jan 31, 2017 at 13:09
4
$\begingroup$

You can also build your own quite easily:

findL[x_, val_] := Max[Select[x, # < val &]];

This selects all the numbers in the list x less than the desired value val and then picks the largest of these. You can, of course plot:

Plot[findL[x, t], {t, 0, 1}]
Improve this answer
$\endgroup$
1
  • $\begingroup$ Suppose the list x is sorted and also val is in a sorted list. How would you improve efficiency over your solution? This is a common alignment problem w event data. $\endgroup$ Commented Sep 29, 2022 at 19:44
2
$\begingroup$

Just a Reap and Sow answer:

fun[c_, lst_] := Reap[Sow[#, Sign[# - c]] & /@ lst, -1, Last[Sort@#2] &][[-1, 1]]

Using data from @MichaelE2:

pts = {0.817389, 0.11142, 0.789526, 0.187803, 0.241361, 0.0657388, 0.542247, 0.231155, 0.396006, 0.700474}; Plot[Quiet@fun[x, pts], {x, 0, 1.5}, Epilog -> {Red, PointSize@Medium, Point[Transpose@{pts, pts}]}]

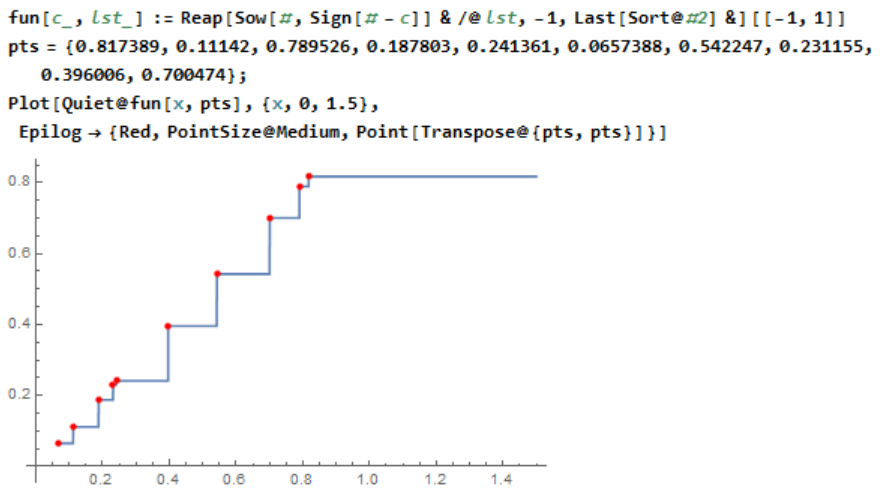
enter image description here

Quiet just deals suppresses message re: no points satisfying criterion (i.e. $x_i<x$). This could be handled by just setting to min of list.

Improve this answer
$\endgroup$
0
$\begingroup$

Using NearestFunction with a custom DistanceFunction is much slower than using one of the built-in distance functions. So, instead, you could use something similar to my LeftNeighbor that returns the value instead:

LeftValue[s_] := LeftValueFunction[s, Nearest[s -> "Index"]] LeftValue[s_, list_] := LeftValue[s][list] LeftValueFunction[s_, nf_][n_] := First @ LeftValueFunction[s, nf][{n}] LeftValueFunction[s_,nf_][list_List] := With[ {n=nf[list][[All,1]]}, s[[n - UnitStep[s[[n]]-list] ]] ]

Here is the setup part of Michael's answer:

SeedRandom[1]; data = Sort @ RandomReal[1, 10^6]; nf = Evaluate @ Interpolation[ Transpose@{-data,data}, InterpolationOrder->0, "ExtrapolationHandler"->{With[{m=-Max[data]},Piecewise[{{-m,#<m}},Indeterminate]&], "WarningMessage"->False} ][-#]&; //RepeatedTiming

{1.14, Null}

And the setup using LeftValue:

lvf = LeftValue[data]; //RepeatedTiming

{0.051, Null}

Creating the LeftValueFunction is much faster. Finally a speed comparison using these functions:

testdata = RandomReal[1, 10^3]; r1 = nf /@ testdata; //RepeatedTiming r2 = lvf[testdata]; //RepeatedTiming r1 === r2

{0.0020, Null}

{0.00018, Null}

True

So, about an order of magnitude speedup.

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.