You could use as input:
Derivative[1, 0][u][2, y]
You can implement the formating rule (Thanks to @Rojo)
Format[Derivative[i_, j_][a_]] := Row[{"\[PartialD]"^(i + j), a}]/ Row[Row[{"\[PartialD]", #}] & /@ {"x"^i, "y"^j}] Format[(h : Derivative[i_, j_][a_])[x0_, y0_]] := RawBoxes@SubscriptBox[RowBox[{MakeBoxes@h, "\[VerticalLine]"}], MakeBoxes@Row[{Row[{x, "=", x0}], ",", Row[{y, "=", y0}]}]]
so that
Derivative[1, 2][u][2, 3]
returns
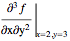
Note that I arbitrary assumed the variables were x,y since I have no way to know from the input alone what the variables are.
This solution also works with input such as
Derivative[1, 2][f][1, x]
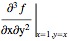
Derivative[0, 0][f][1, 3]
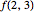
Derivative[2, 0][f][1, 3]
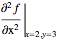
More generally, provided you use (from @Jens see link below)
Derivative /: MakeBoxes[Derivative[\[Alpha]__][f1_][vars__Symbol], TraditionalForm] := Module[{bb, dd, sp}, MakeBoxes[dd, _] ^= If[Length[{\[Alpha]}] == 1, "\[DifferentialD]", "\[PartialD]"]; MakeBoxes[sp, _] ^= "\[ThinSpace]"; bb /: MakeBoxes[bb[x__], _] := RowBox[Map[ToBoxes[#] &, {x}]]; FractionBox[ToBoxes[bb[dd^Plus[\[Alpha]], f1]], ToBoxes[Apply[bb, Riffle[Map[bb[dd, #] &, Select[({vars}^{\[Alpha]}), (# =!= 1 &)]], sp]]]]] D[u[x,y,z],{x,2},{y,3},{z,2}]
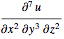
Or extending the above rule to arbitrary dimensions (again from @Rojo I am just a secretary here !)
Format[Derivative[i__][a_]] := Row[{"\[PartialD]"^Total[{i}], a}]/ Times @@ MapIndexed[Subscript["\[PartialD]x", First@#2]^#1 &, {i}]
and
Format[(h : Derivative[i__][a_])[vals__]] := RawBoxes@SubscriptBox[RowBox[{MakeBoxes@h, "\[VerticalLine]"}], ToBoxes@Row[ Riffle[MapIndexed[ Row[{Subscript["x", First@#2], "=", #1}] &, {vals}], ","]]]
so that
Derivative[2, 3, 1][u][1, 2, 3]
returns
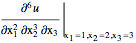
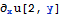
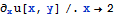

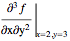
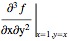
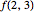
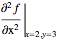
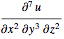
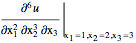
SeriesCoefficient[]. $\endgroup$Derivative[1, 0][u][2, y]? $\endgroup$