How do I find the series solution to the following non-linear second order differential equation up to and including the $x^4$ term and plot the solution curve using Mathematica?
$y''= x + y^2$ (with given initial conditions: $y(0)=0$ and $y'(0)=0$)
$\begingroup$ $\endgroup$
2 
- 1$\begingroup$ What have you tried so far? $\endgroup$Anne– Anne2017-11-20 04:14:08 +00:00Commented Nov 20, 2017 at 4:14
- $\begingroup$ I tried inputting the following code to solve and plot the solution: a = DSolve[{y''[x] == x + (y[x])^2, y[0] == 0, y'[0] == 0}, y[x], x]; Plot[y[x] /. a, {x, -2, 2}], but it did not compute. I have no clue about how to find the series solution either. $\endgroup$Saeed Mohanna– Saeed Mohanna2017-11-20 04:21:26 +00:00Commented Nov 20, 2017 at 4:21
Add a comment |
1 Answer
$\begingroup$ $\endgroup$
1 The series solution is just $\frac{x^3}{6}$ (for these initial conditions)
findSeriesSolution[t_,nTerms_]:=Module[ {pt=0,u,ode,s0,s1,ic,eq,sol,roots}, ic={u[0]->0,u'[0]->0}; ode=u''[t]-t-u[t]^2; s0=Series[ode,{t,pt,nTerms}]; s0=s0/.ic; roots=Solve@LogicalExpand[s0==0]; s1=Series[u[t],{t,pt,nTerms+2}]; sol=Normal[s1]/.ic/.roots[[1]] ] And
seriesSol=findSeriesSolution[x,5]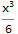 
Plot[x^3/6,{x,0,2}]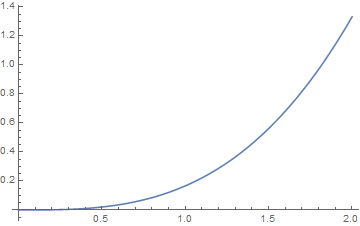 
Compare to NDSolve
ClearAll[u,x] sol=NDSolve[{u''[x]==x+u[x]^2 ,u[0]==0,u'[0]==0},u,{x,0,2}]; Plot[Evaluate[u[x]/.sol],{x,0,2}]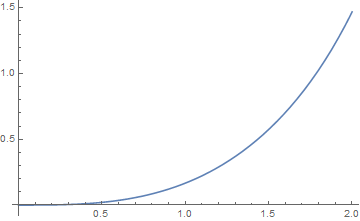 
Verify also using Maple
If you want general series solution for any initial conditions, then replace the line
ic = {u[0] ->0, u'[0] -> 0}; with
ic = {u[0] -> C[1], u'[0] -> C[2]}; In the above function., And now
seriesSol=findSeriesSolution[x,5] $$ \frac{\left(20 c_2 c_1^3+6 c_1^2+5 c_2^3\right) x^7}{1260}+\frac{1}{360} \left(5 c_1^4+10 c_2^2 c_1+4 c_2\right) x^6+\frac{1}{60} \left(5 c_2 c_1^2+c_1\right) x^5+\frac{1}{12} \left(c_1^3+c_2^2\right) x^4+\frac{1}{6} \left(2 c_1 c_2+1\right) x^3+\frac{1}{2} c_1^2 x^2+c_2 x+c_1 $$
You can see that for C[1]=0 and C[2]=0 the above gives $\frac{x^3}{6}$ since all other terms are zero.
- 1$\begingroup$ Ohh ok, thank you so much! $\endgroup$Saeed Mohanna– Saeed Mohanna2017-11-20 04:44:37 +00:00Commented Nov 20, 2017 at 4:44