4
$\begingroup$

I saw some similar posts here, but none of them gave me a solution.

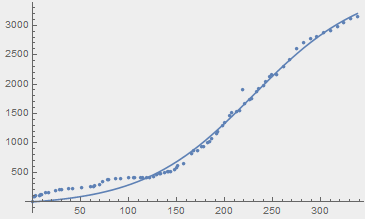
I have this set of data:

data = {{0, 0}, {1, 86}, {2, 86}, {3, 103}, {7, 112}, {8, 122}, {9, 127}, {14, 151}, {17, 157}, {24, 197}, {28, 203}, {30, 208}, {37, 221}, {42, 231}, {51, 233}, {60, 258}, {64, 258}, {65, 281}, {70, 291}, {73, 344}, {78, 372}, {79, 376}, {86, 398}, {92, 390}, {100, 413}, {105, 412}, {106, 408}, {112, 409}, {114, 406}, {119, 410}, {122, 415}, {126, 427}, {129, 460}, {132, 472}, {133, 485}, {137, 495}, {141, 506}, {142, 510}, {144, 519}, {148, 543}, {150, 579}, {151, 607}, {157, 648}, {166, 812}, {168, 862}, {172, 861}, {176, 936}, {178, 942}, {182, 1008}, {184, 1022}, {186, 1074}, {191, 1157}, {193, 1199}, {198, 1298}, {200, 1350}, {205, 1472}, {207, 1519}, {212, 1540}, {215, 1553}, {219, 1906}, {221, 1667}, {226, 1731}, {228, 1760}, {233, 1878}, {235, 1919}, {240, 1971}, {242, 2047}, {247, 2134}, {249, 2155}, {254, 2164}, {261, 2292}, {268, 2416}, {275, 2597}, {282, 2707}, {289, 2775}, {296, 2806}, {303, 2871}, {310, 2917}, {317, 2975}, {324, 3044}, {331, 3108}, {338, 3155}}

And the following model:

sol = ParametricNDSolve[{S'[t] == -a*j[t]*S[t]/12500, q'[t] == a*j[t]*S[t]/12500 - 0.2*q[t], j'[t] == 0.2*q[t] - b*j[t], r'[t] == b*j[t], F'[t] == 0.2*q[t], S[0] == 12500, q[0] == 1, j[0] == 10, r[0] == 0, F[0] == 0}, F, {t, 0, 338}, {a, b}]

Then I am trying to use FindFit to fit parameters a and b

fit = FindFit[data, sol[a, b][t], {a, b}, t]

However, I am getting this message:

FindFit::nrlnum: The function value {<<1>>} is not a list of real numbers with dimensions {82} at {a,b} = {1.,1.}. FindFit::nrlnum: The function value {<<1>>} is not a list of real numbers with dimensions {82} at {a,b} = {1.,1.}.

I tried some other starting values for a and b, but I was unsuccessful. No matter what I try, I get the message that the function value is not real at some point. I am not sure how to get past that. I would appreciate every help I can get.

Improve this question
$\endgroup$

2 Answers 2

Reset to default
3
$\begingroup$

The least square error (or its square root) is

err[a_?NumericQ, b_] := With[{model = (F /. sol)[a, b]}, Norm[data[[All, 2]] - model /@ data[[All, 1]]]]

Let cur = {5, 10}; be the initial parameter guess.

Optimizing the parameter:

fit = FindMinimum[err[a, b], {a, 0, cur[[1]]}, {b, 0, cur[[2]]}] cur = {a, b} /. fit[[2]]; 
{875.34028, {a -> 0.22093849, b -> 0.18673576}} 
Show[Plot[Evaluate[(F /. sol) @@ cur][t], {t, Sequence @@ MinMax[data[[All, 1]]]}], ListPlot[data, PlotRange -> All], PlotRange -> All]

Improve this answer
$\endgroup$
1
  • $\begingroup$ Thank you for your help! $\endgroup$ Commented Jan 9, 2018 at 9:40
2
$\begingroup$

The same result (as given in Coolwater's answer) can be achieved using NMinimize without initial parameter guess:

sol = ParametricNDSolveValue[{ S'[t] == -a*j[t]*S[t]/12500, q'[t] == a*j[t]*S[t]/12500 - 0.2*q[t], j'[t] == 0.2*q[t] - b*j[t], r'[t] == b*j[t], F'[t] == 0.2*q[t], S[0] == 12500, q[0] == 1, j[0] == 10, r[0] == 0, F[0] == 0}, F, {t, 0, 338}, {a, b}, DependentVariables -> {S, q, j, r, F}];

NMinimize shows several warnings

mini = NMinimize[Total@Map[(sol[a, b][#[[1]] ] - #[[2]])^2 &, data],{a, b}] (* {766228., {a -> 0.220993, b -> 0.186785}} *)

but the optimal parameter pair is the same! 

Show[{Plot[ sol[a, b][t] /. mini[[2]] , {t, 0, 338}], ListPlot[data]}]

remark:

FindFit only works with Method->"NMinimize"

fit = Quiet@FindFit[data, sol[a, b][t], {a, b}, t, Method -> "NMinimize"]
Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.