6
$\begingroup$

I want to solve the diffusion equation on a disk centered at (0,0) with a radius of 1. I also want the flux at a radius of 0.8 to be zero. I have this initial condition at time zero:

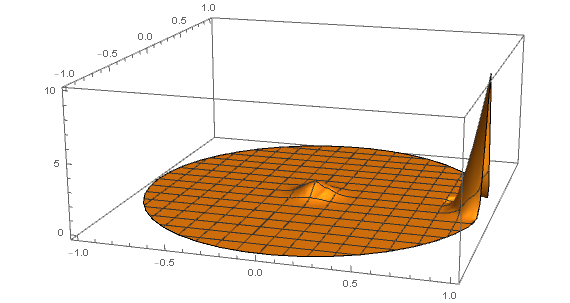
u[x, y, 0] == Exp[(-x^2 - y^2)/0.01] + 10*Exp[-(((x - 1)^2 + (y)^2)/0.01)]

The initial condition looks like this:

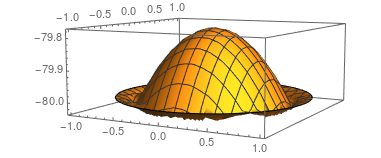
enter image description here

The solution after time 50 looks like this:

enter image description here

The problem is that I expected because the flux is zero at radius of 0.8 then at the distance more than 0.8 from the origin the value of variable u[x,y,t] should be different from that of at distances shorter than 0.8. However, everything looks equilibrated.

Here is the whole code:

sol = NDSolveValue[{ Laplacian[u[x, y, t], {x, y}] == D[u[x, y, t], t] + NeumannValue[0., {x, y} ∈ RegionDifference[Disk[{0, 0}, 1], Disk[{0, 0}, 0.8]]], u[x, y, 0] == Exp[(-x^2 - y^2)/0.01] + 10*Exp[-(((x - 1)^2 + y^2)/0.01)]}, u, {x, y} ∈ Disk[{0, 0}, 1], {t, 0, 50} ] Plot3D[sol[x, y, 0], {x, y} ∈ Disk[{0, 0}, 1], PlotRange -> All]

enter image description here

Improve this question
$\endgroup$
5
  • 3
    $\begingroup$ Here it is necessary to solve two problems: 1) on the disk x^2+y^2<=0.8^2, 2) on the ring 0.8^2<=x^2+y^2<=1. $\endgroup$ Commented Mar 22, 2019 at 14:19
  • $\begingroup$ Thank you. In this link I reduced my real problem and asked a new question. I think I will delete this question then. mathematica.stackexchange.com/questions/193789/… $\endgroup$ Commented Mar 22, 2019 at 20:36
  • $\begingroup$ Why delete? It's an interesting question! $\endgroup$ Commented Mar 25, 2019 at 12:17
  • $\begingroup$ @mjw Yuo are right. At first I thought the other question I asked covers this one. But they seem unrelated. I will not delete the question. $\endgroup$ Commented Mar 25, 2019 at 12:34
  • $\begingroup$ @MOON, Thanks. Hope to have time later to work on it. In any case, looking forward to seeing it develop. $\endgroup$ Commented Mar 25, 2019 at 13:31

1 Answer 1

Reset to default
4
$\begingroup$

Here is a way to have an internal NeumannValue:

We generate a mesh with an internal boundary:

Needs["NDSolve`FEM`"] mesh = ToElementMesh[Annulus[{0, 0}, {8/10, 1}], "RegionHoles" -> None]; mesh["Wireframe"]

enter image description here

The mesh has boundary markers:

mesh["BoundaryElementMarkerUnion"] {1, 2}

Visualize the mesh with it's boundary elements grouped by the markers:

mesh["Wireframe"["MeshElement" -> "BoundaryElements", "MeshElementStyle" -> {Blue, Orange}]]

enter image description here

Solve the equation:

sol = NDSolveValue[{Laplacian[u[x, y, t], {x, y}] == D[u[x, y, t], t] + NeumannValue[1, ElementMarker == 1], u[x, y, 0] == Exp[(-x^2 - y^2)/0.01] + 10*Exp[-(((x - 1)^2 + y^2)/0.01)]}, u, {x, y} \[Element] mesh, {t, 0, 50}];

And visualize the result:

Plot3D[sol[x, y, 50], {x, y} \[Element] mesh, PlotRange -> All]

enter image description here

Improve this answer
$\endgroup$
3
  • $\begingroup$ Why NeumannValue[1,... ? The way I understand the question ("flux at a radius of 0.8 to be zero") it should be NeumannValue[0,... $\endgroup$ Commented Apr 22, 2019 at 10:23
  • $\begingroup$ Though I don't find the question clear. In my interpretation, it could be reformulated as to 2 independent problems. $\endgroup$ Commented Apr 22, 2019 at 10:27
  • $\begingroup$ @andre314, because with `NeumannValue[0,...] you do not see anything. The numerical offset is too small. I also find the question not that clear, so I started with what I gathered and wanted to see what OP had to say. $\endgroup$ Commented Apr 22, 2019 at 11:12

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.