26
$\begingroup$

How to make a function that splits list elements by odd and even positions? Shortest implementation wins. I myself came up with:

splitOdds[x_] := Extract[x, {#}\[Transpose]] & /@ GatherBy[Range@Length@x, OddQ]

And:

splitOdds[x_] := Flatten[Partition[#, 1, 2]] & /@ {x, Rest@x} splitOdds[{a, b, c, d, e, f}] (*{{a, c, e}, {b, d, f}}*)
Improve this question
$\endgroup$
5
  • 4
    $\begingroup$ You can use Span e.g. Range[10][[;; ;; 2]] and Range[10][[2 ;; ;; 2]] $\endgroup$ Commented Mar 16, 2013 at 12:04
  • 1
    $\begingroup$ The title and the text description of this question suggests something completely different. Further users will definitely be confused why you are not gathering even/odd elements, but elements on even/odd positions instead. $\endgroup$ Commented Mar 16, 2013 at 12:19
  • $\begingroup$ @halirutan I agree; I'll change it. $\endgroup$ Commented Mar 16, 2013 at 12:22
  • 1
    $\begingroup$ How about Part[A, #] & /@ GatherBy[Range@Length@lst, OddQ] $\endgroup$ Commented Mar 16, 2013 at 14:00
  • 1
    $\begingroup$ Well, TakeDrop[#, {1, -1, 2}] & since V10.2. $\endgroup$ Commented Mar 17, 2020 at 8:54

12 Answers 12

Reset to default
23
$\begingroup$

A couple for fun:

lst = {a, b, c, d, e, f, g}; Partition[lst, 2, 2, 1, {}] ~Flatten~ {2} 
{{a, c, e, g}, {b, d, f}} 
i = 1; GatherBy[lst, i *= -1 &] 
{{a, c, e, g}, {b, d, f}}

And my Golf entry:

lst[[# ;; ;; 2]] & /@ {1,2} 
{{a, c, e, g}, {b, d, f}}

And here is an anti-Golf "Rube Goldberg" solution:

ReleaseHold[List @@ Dot @@ PadRight[{Hold /@ lst, {}}, Automatic, #]] & /@ Permutations[Range[1, 0, -1]] 
{{a, c, e, g}, {b, d, f}}
Improve this answer
$\endgroup$
3
  • 1
    $\begingroup$ It's brilliant! $\endgroup$ Commented Mar 16, 2013 at 12:21
  • $\begingroup$ @swish Thanks. :-) $\endgroup$ Commented Mar 16, 2013 at 12:22
  • $\begingroup$ Alright. It would be hard to beat but let's see. $\endgroup$ Commented Mar 16, 2013 at 12:27
22
$\begingroup$

Less than sensible, more than pretty, hopefully enjoyable, with a different notion of grouping. Based in part on this question. Gives a new meaning to bubble sort.

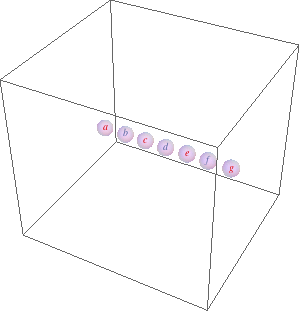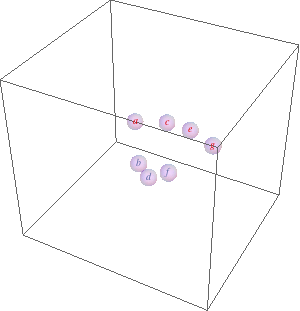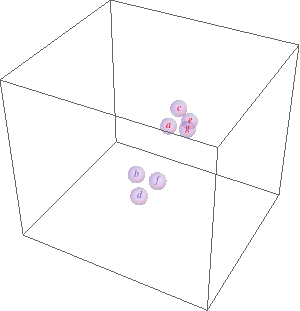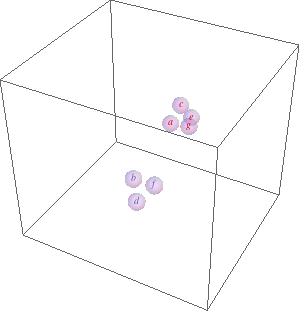
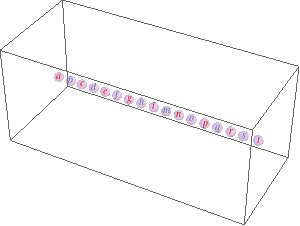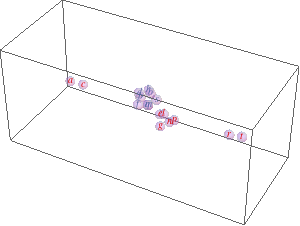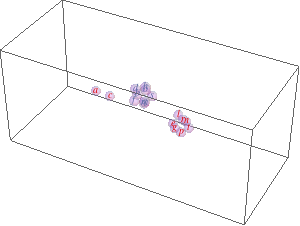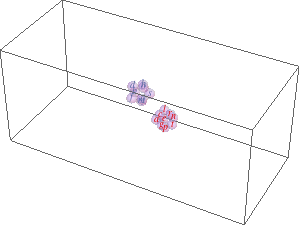
Movie of grouping Movie of grouping

list = {a, b, c, d, e, f, g(*, h, l, m, n, o, p, q, r, s, t*)}; likeElements[list_, {idx_}] /; OddQ[idx] := list[[1 ;; ;; 2]]; likeElements[list_, {idx_}] /; EvenQ[idx] := list[[2 ;; ;; 2]]; coords = Transpose[{Range[#], RandomReal[{-0.01, 0.01}, #], RandomReal[{-0.01, 0.01}, #]}] &@Length[list]; Dynamic[ Refresh[Module[{d}, Graphics3D[GraphicsComplex[ coords -= MapIndexed[ Total[Function[x, (d = # - x)/(d = Sqrt[d.d]) Log@d/2^(2 + 2 Sqrt[d])] /@ Drop[likeElements[coords, #2], Ceiling[#2/2]]] + Total[Function[x, -(d = # - x)/(d = Sqrt[d.d])^2 (d - 1/E) (1 - d/7)/2^(2 + 2 d)] /@ likeElements[coords, #2 + 1]] &, coords], {MapIndexed[Text[Style[#1, ColorData[2][Mod[First[#2], 2]]], First[#2]] &, list], Opacity[0.3], Sphere[Range@Length[list], E^-1]}], PlotRange -> {{-1.5, Length[list] + 1.5}, 4 {-1, 1}, 4 {-1, 1}}] ], UpdateInterval -> 1]]

Tweaking the coefficients slightly changes the behavior, which is also somewhat dependent on the length of the list. Won't win a speed contest.

The two Total[Function...] expressions calculate the new positions based on like elements (same parity) attract (first Total) and unlike repel (second Total).

Improve this answer
$\endgroup$
17
$\begingroup$

You can also use Downsample, which is new in version 9:

lst = {a, b, c, d, e, f, g}; Downsample[lst, 2, #] & /@ {1, 2} (* {{a, c, e, g}, {b, d, f}} *)
Improve this answer
$\endgroup$
4
  • $\begingroup$ Oh neat, one new useful function learned. $\endgroup$ Commented Mar 16, 2013 at 16:28
  • $\begingroup$ Is this function any faster than Part and Span, or Take? $\endgroup$ Commented Mar 17, 2013 at 6:58
  • $\begingroup$ @Mr.Wizard in my quick test, MMA 9.0.1, for packed arrays, better to worse, Downsample- Part- Take, but not for much. For unpacked, the opposite order $\endgroup$ Commented Mar 17, 2013 at 8:01
  • $\begingroup$ Thanks. It sounds like my old friend Part is still a good universal choice. :-) $\endgroup$ Commented Mar 17, 2013 at 8:04
14
$\begingroup$

Since all the sensible answers have already been done...

lst ~(•=#;Cases)~(_/;(•=!•))&/@{!#,#}&[_==_]
Improve this answer
$\endgroup$
5
  • $\begingroup$ Oh great! Now this is going to start an obfuscated mma trend! $\endgroup$ Commented Mar 16, 2013 at 15:02
  • $\begingroup$ This is really great. It's not often I have to do a double-take on syntax. :-O $\endgroup$ Commented Mar 16, 2013 at 15:26
  • 1
    $\begingroup$ Will it rm -rf /* my disk? :) $\endgroup$ Commented Mar 16, 2013 at 16:31
  • 1
    $\begingroup$ @swish I promise to not do anything to your disk ;) $\endgroup$ Commented Mar 16, 2013 at 17:12
  • $\begingroup$ Ok, you've just got my wtf, I mean +1. I still haven't parsed it ... $\endgroup$ Commented Mar 16, 2013 at 22:17
10
$\begingroup$

My way:

lst = {a, b, c, d, e, f, g}; Take[lst, {#, -1, 2}] & /@ {1, 2} 
{{a, c, e, g}, {b, d, f}}
Improve this answer
$\endgroup$
8
  • $\begingroup$ That's mine, just longer. :-p $\endgroup$ Commented Mar 16, 2013 at 12:43
  • $\begingroup$ @Mr.Wizard Ha, I've just seen now that in the docs for Span it says m[[i;;j;;k]] is equivalent to Take[m,{i,j,k}]. Well, let's say that mine is more readable for novice users. $\endgroup$ Commented Mar 16, 2013 at 12:49
  • $\begingroup$ Indeed it is. I'm just poking fun. :-) $\endgroup$ Commented Mar 16, 2013 at 12:54
  • $\begingroup$ By the way, try your hand at a "Rube Goldberg" solution. I had fun with mine, though it could be considerably more complicated... $\endgroup$ Commented Mar 16, 2013 at 12:55
  • $\begingroup$ I just timed these and Take is slightly faster. +1 for pragmatism. $\endgroup$ Commented Mar 16, 2013 at 13:08
7
$\begingroup$

I'll join in with my own version:

splitList[list_] := Pick[list, IntegerDigits[1/6 (-3 - (-1)^#1 + 2^(2 + #1)) &@Length@list, 2], #] & /@ {1, 0} splitList[{a, b, c, d, e, f, g}] (* {{a, c, e, g}, {b, d, f}} *)

This uses the fact that the "selector pattern" or "sieve" for the elements proceeds as

$$1, 10, 101, 1010, 10101,... $$

and the general term (in base 10) for the binary sequence above is $\frac{1}{6}(2^{2+n}-(-1)^n-3)$, where $n$ is the length of your list.

The selector pattern can also be generated more straightforwardly as:

Riffle[ConstantArray[1, Ceiling[Length@list/2]], 0]
Improve this answer
$\endgroup$
1
  • $\begingroup$ Equivalently: splitList[l_List] := With[{n = Length[l]}, Pick[l, IntegerDigits[Ceiling[2 (2^n - 1)/3], 2, n], #] & /@ {1, 0}] $\endgroup$ Commented May 6, 2013 at 6:24
6
$\begingroup$

Here is another one, based on Reap and Sow:

Reap[MapIndexed[Sow[#1, Mod[#2, 2]] &, lst], _, #2 &][[2]]

This one has an advantage to be easily generalizable to more complex conditions, although certainly not the fastest one here.

Improve this answer
$\endgroup$
2
  • $\begingroup$ That looks too complicated. I would write: Reap[# ~Sow~ Mod[#2, 2] & ~MapIndexed~ lst][[2]] $\endgroup$ Commented Mar 16, 2013 at 13:54
  • $\begingroup$ @Mr.Wizard Yes, you can skip the pattern on Reap. But, generally, I am in the habit of keeping it, since I often use Reap with some tags just for safety. $\endgroup$ Commented Mar 16, 2013 at 14:25
5
$\begingroup$

Method 1: GatherBy each element's position (even or odd).

GatherBy[lst, Mod[Position[lst,#],2]&]

{{a, c, e, g}, {b, d, f}}

Method 2: Using ArrayReshape (version 9).

Mathematica graphics

In the following, the MathematicaIcon is used for padding in the reshaping of the array. After the array is reshaped, the icons are removed. Any element can be used in lieu of the MathematicaIcon, provide that one is certain that the padding element is not in the original list.

 ArrayReshape[lst,{Length[lst],2},"\[MathematicaIcon]"]\[Transpose] /."\[MathematicaIcon]"->Sequence[]

Method 3: Check whether each index from MapIndexed is even or odd.

GatherBy[MapIndexed[List,lst],OddQ]/.{x_,{_}}:> x
Improve this answer
$\endgroup$
5
$\begingroup$

Base on Pick:

gather[list_] := Pick[{list, list}, Take[#, Length@list] & /@ {#, RotateLeft[#]} &@ Mod[Range@Ceiling[Length@list, 2], 2], 1]; gather[{a, b, c, d, e, f, g}] 
{{a, c, e, g}, {b, d, f}}
Improve this answer
$\endgroup$
1
  • $\begingroup$ g is in both your output lists! $\endgroup$ Commented Mar 17, 2013 at 4:26
2
$\begingroup$ 
# & @@@ # & /@ GatherBy[MapIndexed[{#, OddQ@#2} &, lst], Last] #[[All, 1]] & /@ GatherBy[MapIndexed[{#, OddQ@#2} &, lst], Last]
Improve this answer
$\endgroup$
1
$\begingroup$ 
list = {a, b, c, d, e, f, g};

Using EveryOther by Wolfram Staff

EveryOther = ResourceFunction["EveryOther"]; EveryOther[list]

{{a, c, e, g}, {b, d, f}}

Using GroupBy

Keys @ Values @ GroupBy[OddQ] @ Association @ MapIndexed[Rule] @ list

{{a, c, e, g}, {b, d, f}}

Improve this answer
$\endgroup$
0
$\begingroup$

This is how i do it:

GetEvenStep[list_] := Partition[list, 2][[All, 1]]

GetOddStep[list_] := Partition[list, 2][[All, 2]]

Be careful, depending on the list you want to split you might want to flip the names!

Improve this answer
$\endgroup$
0

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.