3
$\begingroup$

I am a newbie and I'm trying to use Mathematica to obtain the symbolic Maximum Likelihood Estimation for a cumulative normal distribution. So far I have reached the step where I have the derivative of the log likelihood for both $\mu$ and $\sigma$, i.e. $ \text{score}=\left\{\frac{\partial \text{logL}}{\partial \mu },\frac{\partial \text{logL}}{\partial \sigma }\right\} $, or

$$ \left\{\sum _{i=1}^n -\frac{\sqrt{\frac{2}{\pi }} e^{-\frac{\left(\mu -x_i\right){}^2}{2 \sigma ^2}}}{\sigma \text{erfc}\left(\frac{\mu -x_i}{\sqrt{2} \sigma }\right)},\sum _{i=1}^n \frac{\sqrt{\frac{2}{\pi }} \left(\mu -x_i\right) e^{-\frac{\left(\mu -x_i\right){}^2}{2 \sigma ^2}}}{\sigma ^2 \text{erfc}\left(\frac{\mu -x_i}{\sqrt{2} \sigma }\right)}\right\} $$ The problem is that when I try to solve when these expressions are 0:

Solve[score == {0, 0} && σ > 0, {μ, σ}]

Mathematica tells me that it can't solve it (Solve::nsmet: This system cannot be solved with the methods available to Solve).

Is this really such a hard problem or am I missing something?

Improve this question
$\endgroup$
7
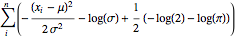
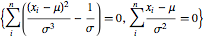
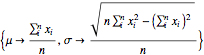
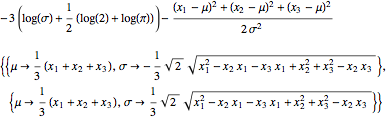
  • $\begingroup$ Try Solve[ Thread[ score={0,0}]...] $\endgroup$ Commented Mar 28, 2013 at 17:17
  • 1
    $\begingroup$ and please typeset mathematica expressions. cf the FAQ. $\endgroup$ Commented Mar 28, 2013 at 17:20
  • $\begingroup$ @chris I tried it with Thread but it still doesn't work, also it works for other distributions such as Poisson, so if Thread is just for the syntax, i don't think I have a syntax issue $\endgroup$ Commented Mar 28, 2013 at 17:39
  • 1
    $\begingroup$ What is your 'cumulative normal distribution'? Do you mean a Normal distribution, or the distribution of the sample sum, or something else? $\endgroup$ Commented Mar 28, 2013 at 17:39
  • 1
    $\begingroup$ Eh? The CDF of the Normal is not the pdf. The MLE is calculated wrt the pdf, not the cdf. $\endgroup$ Commented Mar 28, 2013 at 17:45

1 Answer 1

Reset to default
7
$\begingroup$

Let us try with a Normal distribution. Start by the log normal of it:

ff = PowerExpand[Log@ PDF[NormalDistribution[μ, σ], x], Assumptions -> {σ > 0,μ ∈ Reals, x ∈ Reals}]

Now the log likelihood obey

Q = Sum[ff /. x -> Subscript[x, i], {i, n}]

Mathematica graphics

We can define the condition of stastionarity 

eqn = Thread[D[Q, #] & /@ {σ, μ} == 0]

Mathematica graphics

We need to tell mathematica to expand the sums 

eqn2 = eqn /. Sum[a_, b_] :> sum[Expand[a], b] //. sum[a_ + b_, c_] :> sum[a, c] + sum[b, c] /. sum[a_ b_, c_] :> b sum[a, c] /; FreeQ[b, Subscript[x, i]] /. sum[a_, b_] :> a sum[1, b] /; FreeQ[a, Subscript[x, i]] /. sum -> Sum

Mathematica graphics

now we can solve 

Solve[eqn2, {μ, σ }][[2]]

Mathematica graphics

QED

EDIT

You might want to look at the LogLikelihood function

With this function, taking a definite (n=3) case

Q = LogLikelihood[NormalDistribution[μ, σ], Table[Subscript[x, i], {i, 3}]] Solve[Thread[D[Q, #] & /@ {μ, σ} == 0], {μ, σ}]

Mathematica graphics

With a numerical example:

data = RandomVariate[NormalDistribution[1, 2], 100]; Q = LogLikelihood[NormalDistribution[μ, σ], data]; sol=NSolve[Thread[D[Q, #] & /@ {μ, σ} == 0], {μ, σ}][[2]] (* ==> {μ-> 0.92576, σ-> 2.03064} *) Show[ContourPlot[Q, {μ, -1, 3}, {σ, 1, 3}, ColorFunction -> "Heat"], Graphics[Point[{μ, σ}] /. sol]]

Mathematica graphics

Improve this answer
$\endgroup$
6
  • $\begingroup$ For a cumulative distribution? What sort of density would you suggest this cumulative distribution has? $\endgroup$ Commented Mar 28, 2013 at 17:52
  • $\begingroup$ @chris so this means that the only way to fit a dataset with normcdf is numerical optimization? $\endgroup$ Commented Mar 28, 2013 at 17:54
  • $\begingroup$ @wolfies I guess its a good point: the CDF is not normalized... $\endgroup$ Commented Mar 28, 2013 at 17:55
  • 1
    $\begingroup$ @chris thank you very much for your detailed answer :) $\endgroup$ Commented Mar 28, 2013 at 18:07
  • 1
    $\begingroup$ The problem is that a normal cumulative distribution is not a distribution as its integral diverges. $\endgroup$ Commented Mar 29, 2013 at 6:38

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.