1
$\begingroup$

Suppose that I have matrix matT1 at time t and matT2 at time t+1:

matT1 = { {0.98, 0.95, 1.00, 0.85, 1.40}, {1.46, 0.36, 0.96, 0.15, 0.97}, {0.24, 1.20, 1.40, 0.96, 0.46}, {1.10, 1.30, 0.03, 0.81, 0.53}, {1.30, 1.50, 1.30, 0.51, 0.42} }; matT2 = { {0.44, 1.00, 0.77, 1.20, 0.61}, {0.58, 0.57, 0.65, 0.19, 1.00}, {1.40, 0.14, 1.20, 1.40, 0.96}, {1.40, 0.95, 0.74, 0.56, 0.47}, {0.98, 0.45, 1.30, 0.34, 0.25} };

Note that these matrices represent two different weighted directed graphs with 5 vertices. Elements of these two matrices are assigned to one of the five states s1=[0, 0.5], s2=(0.5, 1], s3=(1, 1.5] etc.

r1T1=BoolEval[0<= matT1<=0.5]/.{1->s1}; r2T1=BoolEval[0.5<matT1<= 1]/.{1-> s2}; r3T1=BoolEval[1<matT1<=1.5]/.{1 -> s3}; r4T1=BoolEval[1.5<matT1<=2]/.{1 -> s4}; r5T1=BoolEval[2<matT1<=2.5]/.{1 -> s5}; matT1S = r1T1 + r2T1 + r3T1 + r4T1 + r5T1 // MatrixForm r1T2=BoolEval[0<=matT2<=0.5]/.{1 -> s1}; r2T2=BoolEval[0.5<matT2<=1]/.{1 -> s2}; r3T2=BoolEval[1<matT2<=1.5]/.{1 -> s3}; r4T2=BoolEval[1.5<matT2<=2]/.{1 -> s4}; r5T2=BoolEval[2<matT2<=2.5]/.{1 -> s5}; matT2S = r1T2 + r2T2 + r3T2 + r4T2 + r5T2 // MatrixForm

respectively yield:

matT1S = { {s2, s2, s2, s2, s3}, {s3, s1, s2, s1, s2}, {s1, s3, s3, s2, s1}, {s3, s3, s1, s2, s2}, {s3, s3, s3, s2, s1} }; matT2S = { {s1, s2, s2, s3, s2}, {s2, s2, s2, s1, s2}, {s3, s1, s3, s3, s2}, {s3, s2, s2, s2, s1}, {s2, s1, s3, s1, s1} };

We then derive a map of transition from matT1S to matT2Sby manually comparing the states in both matrices.

Clear[n, states, map]; n = Length[matT2S]; states = {s1, s2, s3, s4, s5}; map = {}; Do[ If[matT1S[[i, j]] == states[[1]] && matT2S[[i, j]] == states[[2]], AppendTo[map, {i, j}] ], {i, n}, {j, n} ] Length[map] (* gives 0 *)

For each pair of states, I run the above code to obtain the following map:

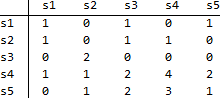
enter image description here

Rows are associated with time t and columns with t+1. This map illustrates that, out of 3 links in state s1 at time t, 1 remains in s1 at t+1, and 1 moves to s3 at t+1 and 1 moves to s5 at t+1. Other numbers in the map should be read likewise. Using this map,

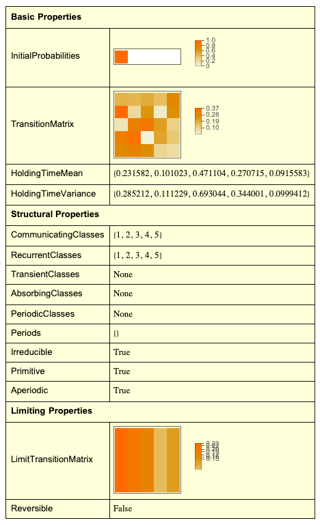
traMap={ {1,0,1,0,1}, {1,0,1,1,0}, {0,2,0,0,0}, {1,1,2,4,2}, {0,1,2,3,1} }; transMatrix= DiagonalMatrix[1/Total[traMap, {2}]].traMap

A row-stochastic transition matrix as:

transMatrix = { {1/3, 0, 1/3, 0, 1/3}, {1/3, 0, 1/3, 1/3, 0 }, {0, 1, 0, 0, 0 }, {1/10, 1/10, 1/5, 2/5, 1/5}, {0, 1/7, 2/7, 3/7, 1/7} };

and

MatrixPower[transMatrix, 100]

produces the following limiting distribution:

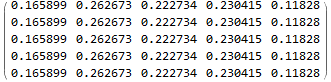
enter image description here

This limiting distribution translates the current vector (3, 3, 2, 10, 7) to (0.17, 0.26, 0.22, 0.23, 0.12)*(3, 3, 2, 10, 7).

My question: Although I found out the transition, I do not know which linkages are in each state in the final period t+100. I like to know the specific linkages associated the new distribution (0.17, 0.26, 0.22, 0.23, 0.12)*(3, 3, 2, 10, 7).

Would it be possible to write a function transMatrix[matrixT_,matrixT1_]:=... to produce: a transition matrix (row stochastic matrix), a final distribution of the linkages across three states, and subsets of the linkages across each state?

Improve this question
$\endgroup$
2
  • 1
    $\begingroup$ Can you give an example of a few "linkages", say, of length three ( $t+3$ .) $\endgroup$ Commented Aug 29, 2020 at 15:35
  • $\begingroup$ @Anton Antonov: I have only two time periods and 3 states in the example. Therefore, there is no length-3 linkage. Max linkage has length-2. From s1 to s2, the set of binary links with vertex names is {{2,2},{4,3},{3,5}} because I have a total of 5 vertices; from s2 to s3, the set of links is {{3,4},{1,4}}; and from s3 to s1, the set is {{3,2},{5,2}}. To find the binary links associated with the limiting distribution, we need to identify the specific binary links that is likely to end up with the state implied by the limiting distribution. I hope I am not confusing you. $\endgroup$ Commented Aug 29, 2020 at 16:28

2 Answers 2

Reset to default
1
$\begingroup$

A more streamlined way to produce the matrices in OP (not an answer):

ClearAll[toStates] toStates[t_, s_, m_] := Map[s[[Total[1 - UnitStep[t - #]]]] &, m, {2}] thresholds = {0, .5, 1., 1.5}; states = {s1, s2, s3}; m1S = toStates[thresholds, states, matT1]; m2S = toStates[thresholds, states, matT2]; {m1S, m2S} == {matT1S, matT2S} 
 True 
maP[m1_, m2_, st_] := PadRight[KeySort[GroupBy[ Join @@ (Transpose /@ Transpose[{m1, m2}]), First -> Last, KeySort[Counts[#]] /@ st /. _Missing -> 0 &]] /@ st /. _Missing -> {0}] maP[m1S, m2S, states] TeXForm @ MatrixForm @ %

$\left( \begin{array}{ccc} 2 & 3 & 1 \\ 3 & 5 & 2 \\ 2 & 4 & 3 \\ \end{array} \right)$

tm = Normalize[#, Total] & /@ map; TeXForm @ MatrixForm @ tm

$\left( \begin{array}{ccc} \frac{1}{3} & \frac{1}{2} & \frac{1}{6} \\ \frac{3}{10} & \frac{1}{2} & \frac{1}{5} \\ \frac{2}{9} & \frac{4}{9} & \frac{1}{3} \\ \end{array} \right)$

Improve this answer
$\endgroup$
8
  • $\begingroup$ Thank you for a nice function. It works as expected if all the elements in map are positive, but it does not work if there is a zero transition from, say, s1 to s2. I will edit my question with a new pair of matrices and the intervals. You may try your Code with the example. $\endgroup$ Commented Aug 30, 2020 at 13:48
  • $\begingroup$ @Tugrul, the new version of map should work for cases with zero transitions. $\endgroup$ Commented Aug 30, 2020 at 14:02
  • $\begingroup$ Thank you very much. I also edited the question with a new matrix. I will try it and let you know. $\endgroup$ Commented Aug 30, 2020 at 14:19
  • $\begingroup$ Your map function has a problem. It always gives me 3 by 3 matrix in the original example matrix I gave, although I run the code with a 5 by 5 matrix as in the edited question. It looks like the map code does not accept the new matrices m1S and m2S. $\endgroup$ Commented Aug 30, 2020 at 14:41
  • $\begingroup$ @Tugrul, hope the new version works in general. $\endgroup$ Commented Aug 30, 2020 at 15:29
2
$\begingroup$

I am not sure I understand the question. It seems to me that you can make the transition matrix by making the graph adjacency matrix row stochastic.

Here is an example with question’s matT1:

matT1rs = DiagonalMatrix[1/Total[matT1, {2}]].matT1; Total[matT1rs, {2}] (* {1., 1., 1., 1., 1.} *) MarkovProcessProperties[DiscreteMarkovProcess[{1, 0, 0, 0, 0}, matT1rs]]

enter image description here

Improve this answer
$\endgroup$
1
  • $\begingroup$ It seems that I could not explain the problem well. I will edit the question to be more precise. Thanks. $\endgroup$ Commented Aug 28, 2020 at 13:00

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.