3
$\begingroup$

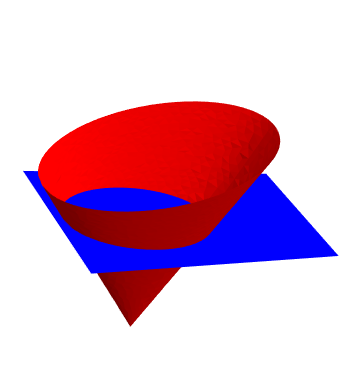
I am encountering difficulties in finding the intersection between a region defined as an elliptical cone and another region. For the time being the other region is a simple InfinitePlane. I plan to use the intersection region and its boundary to perform all sort of operations on it, such as determine the surface area, curvature, centroid, integrate a signal, etc.

I define the cone as follows

ConusElipsorum[apex_, centrum_, semiMaj_, semiMin_, majVec_, minVec_, u_, v_] := Module[{e}, e = centrum + semiMaj majVec Cos[u] + semiMin minVec Sin[u]; (* elipsum *) (1 - v) apex + v e (* conus *) ]

Points apex and centrum are the apex of the cone and the center of its base. The semi-axes of the base are semiMaj and semiMin and the orientation of the base is given by majVec along the major axis and minVec along the minor axis. To make the cone right I choose majVec to be normal to the unit vector along apex - centrum and minVec is given by the right-hand rule between these two vectors.

I define the conic region as

p = {10, 0, 0}; k = {0, 0, 5}; n = Normalize[p - k]; (* vector along cone axis *) l = Normalize[{0.5, 0, 1}] (* vector normal to cone axis and along major axis *) m = Cross[n, l] (* vector normal to both cone axis and the major axis *) pr1 = ParametricRegion[ConusElipsorum[p, k, 5.5, 3, l, m, u, v], {{u, 0, 2 Pi}, {v, 0, 1}}];

the plane region as

pr2 = InfinitePlane[{{0, 0, 0}, {0, 1, 0}, {1, 0, 1}}];

and I plot them with

Show[Region[Style[pr1, Red]], Region[Style[pr2, Blue]]]

Cone region (red) and InfinitePlane region (blue)

I calculate their intersection as

ri=RegionIntersection[pr1, pr2]

that returns

BooleanRegion[#1 && #2 &, {ParametricRegion[{{10 (1 - v) + (0. + 2.45967 Cos[u]) v, v (0. - 3. Sin[u]), (5. + 4.91935 Cos[u]) v}, 0 <= u <= 2 \[Pi] && 0 <= v <= 1}, {u, v}], ParametricRegion[{{11 (1 - v) + (3. + 2.45967 Cos[u]) v, 1 - v + v (3. - 3. Sin[u]), 1 - v + (8. + 4.91935 Cos[u]) v}, 0 <= u <= 2 \[Pi] && 0 <= v <= 1}, {u, v}]}]

This is where I get stuck. I have tried to plot the intersection with Region[ri] and Mathematica stalls in this cell evaluation. I have read (most of) the Mathematica documentation on manipulating regions to no avail. I believe I am missing something fundamental but I don't know where to start.

Can you help? Thank you.

B

Improve this question
$\endgroup$

1 Answer 1

Reset to default
2
$\begingroup$

Mathematica's region / Boolean CSG stuff is sadly very buggy, even in some simple cases like this where you really wouldn't expect it. I'm hoping it improves in future versions. To work around this I discretize the mesh into polygons and intersect each polygon individually, building up a list of EmptyRegion[3] and lines. The empty regions are discarded.

mesh1 = DiscretizeRegion@pr1; prims = MeshPrimitives[mesh1, 2]; intersections = DeleteCases[RegionIntersection[#, pr2] & /@ prims, EmptyRegion[_]]; curveregion = RegionUnion[intersections]; Graphics3D[{{Red, EdgeForm[None], mesh1}, Blue, pr2, Yellow, Thick, intersections}, BoxRatios -> 1] RegionMeasure[curveregion] (* result: 19.3212 *)

ellipse cone plane intersection

Of course, this just gets you the curve around the edge of the cone. If you want the surface on the interior for things like area / integration etc., then you'll need to construct a polygon from the intersection coordinates. I extract the coordinates from the line and perform a FindShortestTour because they need to be reordered as we wind around the curve. I do not display the plane due to z-fighting in the graphics.

interiorsurface = Polygon[#[[Last@FindShortestTour@#]]&@intersections[[All,1,1]]]; centroid = RegionCentroid[interiorsurface]; Graphics3D[{{Red, EdgeForm[None], mesh1}, Yellow, Thick, intersections, interiorsurface, Green, PointSize[.02], Point[centroid]}, BoxRatios -> 1] RegionMeasure[interiorsurface] (* result: 25.2026 *)

cone ellipse intersection with surface and centroid

Improve this answer
$\endgroup$
1
  • $\begingroup$ Thank you @flinty ! That's a very elegant solution. I didn't know any of the meshing functions that you used so this was a great learning experience. The meshing operation helps a lot because the goal is to replace the elliptic basis of the cone with some general closed curve - I think we called that a ruled surface in descriptive geometry. I'm off to intersecting the cone with a sphere and extracting the cap. I'll report the results here when done. Cheers! $\endgroup$ Commented Oct 5, 2020 at 4:31

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.