I am totally new to Mathematica, so if this is a simple googleable question, I am sorry
I have this expression: $\left(e^{i \text{p1} x}-e^{-i \text{p1} x}\right) \left(e^{i \text{p2} x}-e^{-i \text{p2} x}\right) \left(e^{i \text{p3} x}-e^{-i \text{p3} x}\right) \left(e^{i \text{p4} x}-e^{-i \text{p4} x}\right) $
(Exp[I*p1 *x] - Exp[-I*p1 *x]) (Exp[I*p2 *x] - Exp[-I*p2 *x]) (Exp[I*p3 *x] - Exp[-I*p3 *x]) (Exp[I*p4 *x] - Exp[-I*p4 *x]) I want to see it as a sum of $e^{iax}$ terms. Expand does that, but it gives: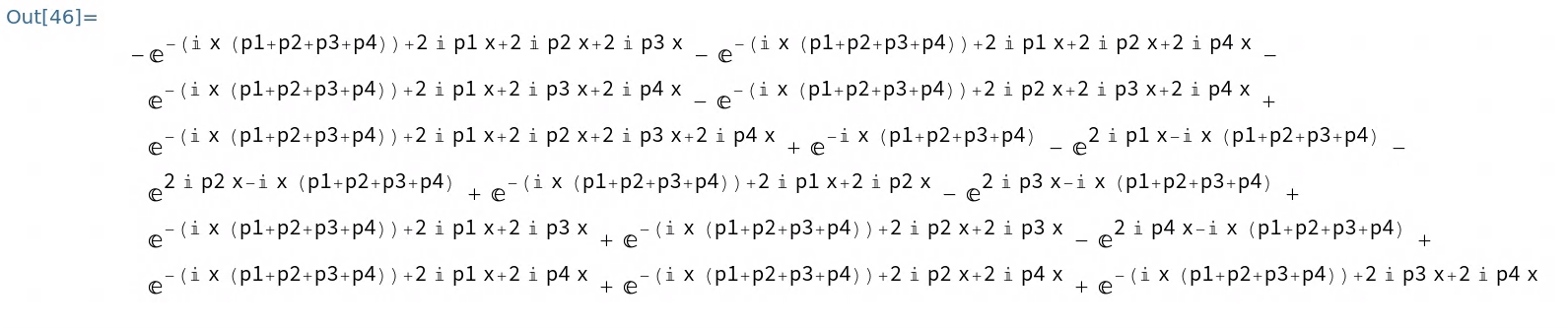 
which could be further simplified as you can see by looking at it. How do I change these terms with minus signs(for eg, $p1-p2+p3-p4$) in the exponential and hence shorter?
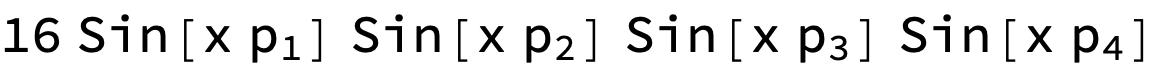
FullSimplify? $\endgroup$Expandyou get $e^{-i p_1 x-i p_2 x-i p_3 x-i p_4 x}-e^{i p_1 x-i p_2 x-i p_3 x-i p_4 x}-\cdots-e^{-i p_1 x+i p_2 x+i p_3 x+i p_4 x}+e^{i p_1 x+i p_2 x+i p_3 x+i p_4 x}$. WithFullSimplifyyou get $16 \sin \left(p_1 x\right) \sin \left(p_2 x\right) \sin \left(p_3 x\right) \sin \left(p_4 x\right)$. $\endgroup$