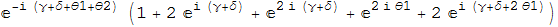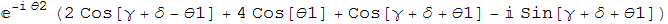4
$\begingroup$

I have a sum of exponentials that I'd like to simplify. The issue is when I use Simplify, Mathematica loves to factor out one exponential factor. See below: $$e^{-i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta +\text{$\theta $1}+\text{$\theta $2})} \left((e^{i (d (\text{kx1}+\text{kx2})+2 \beta )}+2 e^{i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta )}+e^{i (d (\text{kx1}+\text{kx2})+2 (\beta +\gamma +\delta ))}+2 e^{i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta +2 \text{$\theta $1})}+e^{i (d (\text{kx1}+\text{kx2})+2 (\beta +\text{$\theta $1}))}\right....))$$

Otherwise, when I try to Expand it I get $$e^{i (d (\text{kx1}+\text{kx2})+2 \beta )-i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta +\text{$\theta $1}+\text{$\theta $2})}+2 e^{i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta )-i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta +\text{$\theta $1}+\text{$\theta $2})}+e^{i (d (\text{kx1}+\text{kx2})+2 (\beta +\gamma +\delta ))-i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta +\text{$\theta $1}+\text{$\theta $2})}+2 e^{i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta +2 \text{$\theta $1})-i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta +\text{$\theta $1}+\text{$\theta $2})}+e^{i (d (\text{kx1}+\text{kx2})+2 (\beta +\text{$\theta $1}))-i (d (\text{kx1}+\text{kx2})+2 \beta +\gamma +\delta +\text{$\theta $1}+\text{$\theta $2})}$$

Any help on how to "simplify" correctly would be greatly appreciated. Note, Refine does nothing in my case.

Improve this question
$\endgroup$
1
  • 11
    $\begingroup$ Posting executable Mathematica code for copy&paste would be helpful. $\endgroup$ Commented Jul 19, 2012 at 20:28

1 Answer 1

Reset to default
7
$\begingroup$

Taking the expression you get when Expand is applied, Simplify and FullSimplify work nicely if one isn't going to generalize it to much.

expr = E^( I( d(kx1 + kx2) + 2β) - I ( d(kx1 + kx2) + 2β + γ + δ + θ1 + θ2)) + 2 E^( I( d(kx1 + kx2) + 2β + γ + δ) - I( d(kx1 + kx2) + 2β + γ + δ + θ1 + θ2)) + E^( I( d(kx1 + kx2) + 2(β + γ + δ)) - I( d(kx1 + kx2) + 2β + γ + δ + θ1 + θ2)) + 2 E^( I( d(kx1 + kx2) + 2β + γ + δ + 2θ1) - I( d(kx1 + kx2) + 2β + γ + δ + θ1 + θ2)) + E^( I( d(kx1 + kx2) + 2(β + θ1)) - I( d(kx1 + kx2) + 2 β + γ + δ + θ1 + θ2));

We can apply Simplify :

Simplify[ expr]

enter image description here

or FullSimplify

FullSimplify[expr]

enter image description here

If we assume another conditions (the second argument of Simplify or FullSimplify) we can get a simpler expression, e.g. assuming θ1 == θ2 and γ + δ == 0 yields : 

Simplify[ expr, θ1 == θ2 && γ + δ == 0] 
3 + 4 E^(-2 I θ2)

Edit 1

Taking into account the comments beneath I could do the task in another way, since it seems you just don't like the factorizing effect of Simplify on the whole expression. Therefore we can write the expression in the List form, then simplify every term seperately and finally write the terms as a sum :

Plus @@ Simplify[ List @@ expr] 
E^(I ( γ + δ - θ1 - θ2)) + 2 E^(I ( θ1 - θ2)) + E^(-I ( γ + δ - θ1 + θ2)) + 2 E^(-I (θ1 + θ2)) + E^(-I ( γ+ δ + θ1 + θ2))

or even better map Simplify over the expression, simply :

Simplify /@ expr

since it returns the same :

Plus @@ Simplify[List @@ expr] == Simplify /@ expr 
True

Edit 2

There are many ways to do things in Mathematica, here is another useful one : 

expr /. Power[a_, b_] :> Power[a, Simplify[b]]

or if you want to simplify only exponentials :

expr /. E^(a_) :> E^Simplify[a]

They return the results as mapping Simplify over the expression, e.g. :

Simplify /@ expr == expr /. Power[a_, b_] :> Power[a, Simplify[b] 
True
Improve this answer
$\endgroup$
6
  • 2
    $\begingroup$ Simplifies nicely to trig functions, if you actually type in \[ImaginaryI] instead of i. $\endgroup$ Commented Jul 19, 2012 at 20:49
  • $\begingroup$ @Guillochon Do you mean when using ExpToTrig? $\endgroup$ Commented Jul 19, 2012 at 20:57
  • $\begingroup$ @CHM FullSimplify will actually convert to trig automatically, if it can. $\endgroup$ Commented Jul 19, 2012 at 22:24
  • $\begingroup$ @Guillochon I was asking because I get the same result when I use FullSimplify on expr/. "i" -> \[ImaginaryI]. $\endgroup$ Commented Jul 19, 2012 at 22:30
  • $\begingroup$ Here's the thing. I do NOT want it to factor out one of the exponentials. Secondly, my list of exponentials is really long, so FullSimplify would take a really long time. Let me clarify that all I wanted was basically to simplify each individual exponential, if that makes sense. $\endgroup$ Commented Jul 24, 2012 at 21:10

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.