11
$\begingroup$

Hi I am new to using Mathematica, so am not too confident. I am essentially trying to model vibrations of a guitar sound board for a project. It would be great to get some visualisations of the eigenfunctions. Apologies if some of the Qs are simple, I am learning as I go.

I started with finding a simplified equation for the guitar outline (sort of avocado shaped).

PolarPlot[4 + 1/2*Cos[t] + 3/2*Cos[2*t], {t, 0, 2*Pi}, PlotRange -> {{-6, 6}, {-6, 6}}]

I've switched to cartesian coordinates here and included a circle to account for the soundhole.

tocartesian = {t -> ArcTan[x, y], r -> Sqrt[x^2 + y^2]} guitarregion = ImplicitRegion[ r < 4 + 1/2*Cos[t] + 3/2*Cos[2*t] /. tocartesian // Simplify, {x, y}] soundholeregion = ImplicitRegion[r < 1 /. tocartesian // Simplify, {x, y}] wholeregion = RegionDifference[guitarregion, soundholeregion] DiscretizeRegion[wholeregion, PrecisionGoal -> 8] RegionMeasure[%]

Avocado Guitar Mesh

This produces a mesh that is slightly cut off at the top and I am unsure why...

Next, after looking at some other queries on stack exchange I have seen this code utilising the inbuilt functions on Mathematica (Numerically solving Helmholtz equation in 2D for arbitrary shapes):

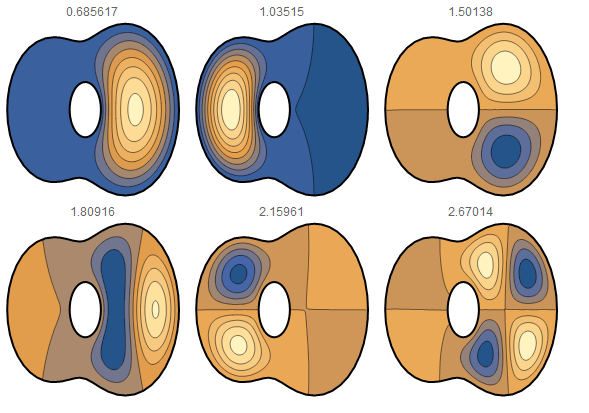
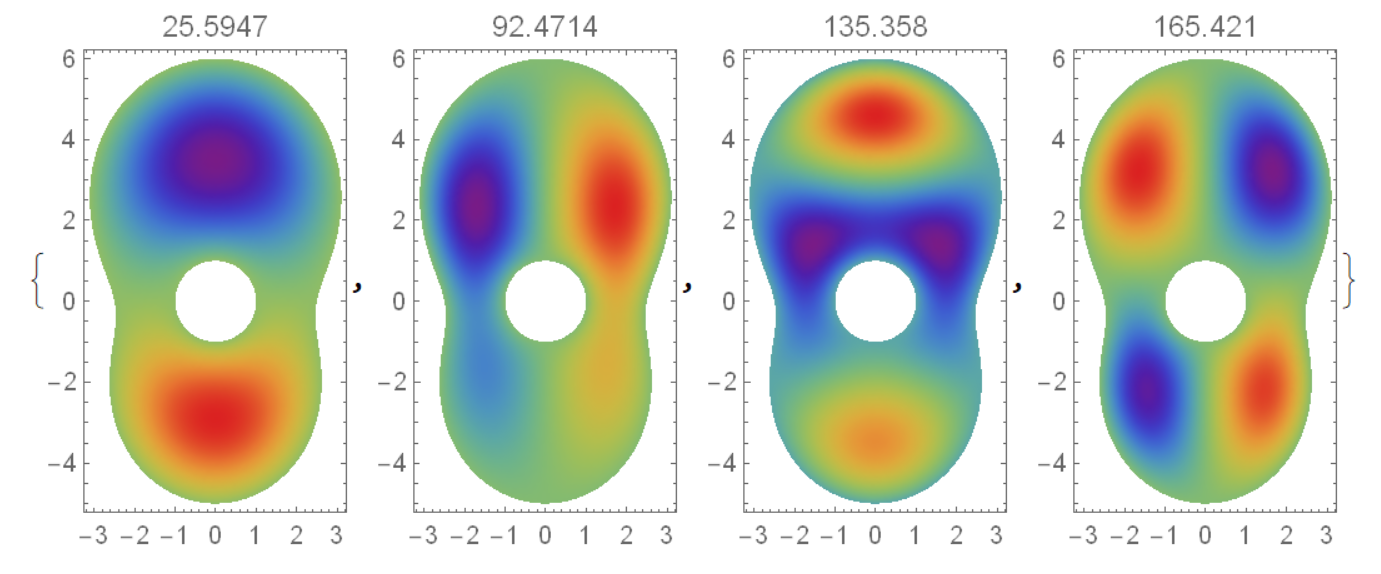
region = {eigenvalues[region], eigenfunctions[region]} = NDEigensystem[{-Laplacian[u[x, y], {x, y}], DirichletCondition[u[x, y] == 0, True]}, u[x, y], {x, y} \[Element] region, 6]; Grid[Partition[ Table[Show[{ContourPlot[ eigenfunctions[region][[j]], {x, y} \[Element] region, Frame -> None, PlotPoints -> 60, PlotRange -> Full, PlotLabel -> eigenvalues[region][[j]]], RegionPlot[region, PlotStyle -> None, BoundaryStyle -> {Black, Thick}]}], {j, 1, Length[eigenvalues[region]]}], 3]]

Does this only work for arbitrary/ symmetrical shapes? If I input my region as

region = wholeregion

It comes up with the message I should use 'ToElementMesh'. I am quite stuck really as to how to proceed since I don't fully understand the software. Any advice/ information would be really appreciated. Maybe this is just not possible!

Improve this question
$\endgroup$
3
  • $\begingroup$ Welcome to Mathematica.SE! I suggest the following: 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Take the tour! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! $\endgroup$ Commented Mar 20, 2021 at 18:16
  • 2
    $\begingroup$ As a guitarist, I do have to point out that this isn't even slightly representative of how a guitar top would behave. What most affects a guitar top's response is the bracing underneath it, not the top itself. It's like modelling a skyscraper by assuming it's just a box made of glass and ignoring all the concrete and steel inside; or modelling a tree trunk by assuming it's just a hollow paper tube. Of course this would make the model much more complicated, but it depends if it's a purely mathematical exercise or if you might actually want to do something based on the results. $\endgroup$ Commented Mar 20, 2021 at 21:33
  • 1
    $\begingroup$ @Graham myself also! Yes, I am aware. I am doing this as an exercise and have noted this is not the most realistic simulation. Including bracing is beyond the scope of the project, but I will definitely try including this in time. $\endgroup$ Commented Mar 21, 2021 at 0:20

2 Answers 2

Reset to default
8
$\begingroup$

You can use FEMAddOns to join two boundary meshes and create an ElementMesh. The following will issue a warning that seems to be safely ignored.

(*Uncommented the following function if FEMAddOns not installed*) (*ResourceFunction["FEMAddOnsInstall"][]*) Needs["FEMAddOns`"]; ℛ = ParametricRegion[(4 + 1/2*Cos[t] + 3/2*Cos[2*t]) {Cos[t], Sin[t]}, {{t, 0, 2 π}}]; (bmeshg = ToBoundaryMesh[ℛ])["Wireframe"]; (bmeshh = ToBoundaryMesh[soundholeregion])["Wireframe"]; (bmesh = BoundaryElementMeshJoin[bmeshg, bmeshh])["Wireframe"] (mesh = ToElementMesh[bmesh, "RegionHoles" -> {{0, 0}}])["Wireframe"]

Boundary and element mesh

Now, the system can be solved.

region = mesh; {eigenvalues[region], eigenfunctions[region]} = NDEigensystem[{-Laplacian[u[x, y], {x, y}], DirichletCondition[u[x, y] == 0, True]}, u[x, y], {x, y} ∈ region, 6]; Grid[Partition[ Table[Show[{ContourPlot[ eigenfunctions[region][[j]], {x, y} ∈ region, Frame -> None, PlotPoints -> 60, PlotRange -> Full, PlotLabel -> eigenvalues[region][[j]]], RegionPlot[region, PlotStyle -> None, BoundaryStyle -> {Black, Thick}]}], {j, 1, Length[eigenvalues[region]]}], 3]]

Eigen solution

Improve this answer
$\endgroup$
3
  • $\begingroup$ Nice approach (+1), but if we are looking for frequencies of wooden plate, then we should use another model. $\endgroup$ Commented Mar 20, 2021 at 14:37
  • $\begingroup$ @AlexTrounev Thanks! I do not disagree. I did not delve into the physics, but merely offered a way to get the OP's desired shape into an ElementMesh. $\endgroup$ Commented Mar 20, 2021 at 17:46
  • $\begingroup$ But you are very good scientist and therefore you understand that there are 3D modes in a body and 2D modes on wooden plates. Also all modes should be scaled to the real size of the body. $\endgroup$ Commented Mar 20, 2021 at 17:53
7
$\begingroup$

We can use FEM to discretize region and DiscretizeRegion[] as well

Needs["NDSolve`FEM`"] tocartesian = {t -> ArcTan[y, x], r -> Sqrt[x^2 + y^2]}; guitarregion = ImplicitRegion[ 1 <= r <= (4 + 1/2*Cos[t] + 3/2*Cos[2*t]) /. tocartesian // Simplify, {x, y}]; mesh = ToElementMesh[guitarregion, MaxCellMeasure -> .01] {mesh["Wireframe"], DiscretizeRegion[guitarregion]}

Figure 1

If we need frequencies of the wooden top plate, then we should apply some elastic model like we did here, then we have

Y = 10.8*10^9; nu = 31/100; rho = 500; h = .003; d =(11/50)^2 10^4 Sqrt[Y h^2/(12 rho (1 - nu^2))];Ld2 = {Laplacian[-d u[x, y], {x, y}] + v[x, y], -d Laplacian[v[x, y], {x, y}]}; {vals, funs} = NDEigensystem[{Ld2, DirichletCondition[u[x, y] == 0, True]}, {u, v}, Element[{x, y}, mesh], 5]; Table[DensityPlot[Re[funs[[i, 1]][x, y]], {x, y} \[Element] mesh, PlotRange -> All, PlotLabel -> vals[[i]]/(2 Pi), ColorFunction -> "Rainbow", AspectRatio -> Automatic], {i, 2, Length[vals]}]

The standard height of YAMAHA guitar top is of about 50 cm, therefore we scale it to 11, since we use mesh of this height. Figure 2

Improve this answer
$\endgroup$
3
  • $\begingroup$ Thank you for your help - this is invaluable! $\endgroup$ Commented Mar 20, 2021 at 15:49
  • $\begingroup$ I get the issue that lists{vals, funs} and NDEigensystem are not the same shape.. Am I missing a step? Thanks $\endgroup$ Commented Mar 20, 2021 at 16:00
  • $\begingroup$ @sp96 thank you for testing, code has been updated, just put Needs["NDSolveFEM"] at the first line. $\endgroup$ Commented Mar 20, 2021 at 16:20

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.