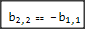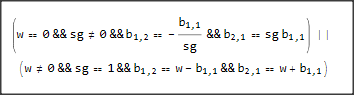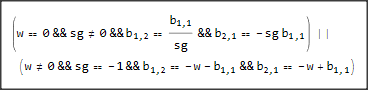0
$\begingroup$

When I read an article by Garbe, where have an eigenmatrix $$B M_i + M_i B^T=\lambda_iM_i$$ and have the following eigenmatrices and eigenvalues:

$$ M_0=\begin{bmatrix} 0 & 1 \\ -1 & 0\end{bmatrix},M_1=\begin{bmatrix} \frac{1}{\sqrt{Xg^2-1}} & 0 \\ 0 & -\sqrt{Xg^2-1}\end{bmatrix}, M_{\pm}=\begin{bmatrix} \frac{1}{\sqrt{Xg^2-1}} & \pm1 \\ \pm1 & \sqrt{Xg^2-1}\end{bmatrix}\\ \lambda_0=\lambda_1=0, \lambda_{\pm}=\pm2\omega_0\sqrt{Xg^2-1}$$

I tried to solve the matrix equation, hoping to get the same result as the article, but I didn't have any beneficial results.

Below is my code for the question

B = {{0, w0}, {w0(X g^2-1), 0}} M = Array[m, {2, 2}] λ = {{λ1, λ2}, {λ3, λ4}} sol = Solve[B.M + M.B\[Transpose] == λ M, Flatten[M]]

It's not producing the results I want.

Any help is much appreciated.

Improve this question
$\endgroup$
2
  • $\begingroup$ "i read an article" - then, please include a link to this article in your question. $\endgroup$ Commented Aug 6, 2022 at 8:16
  • $\begingroup$ I cannot understand the derivation in Louis Garbe's article (arxiv.org/pdf/1910.00604.pdf) about how to solve the covariance matrix equation in Appendix_Dissipative dynamics. $\endgroup$ Commented Aug 6, 2022 at 9:15

1 Answer 1

Reset to default
1
$\begingroup$

The first equation yields:

bb = Array[Subscript[b, #1, #2] &, {2, 2}]; sq = Sqrt[x g^2 - 1]; m0 = {{0, 1}, {-1, 0}}; Reduce[bb . m0 + m0 . Transpose[bb] == 0, Flatten@bb]

enter image description here

With this, the second equation does not give any new information:

bb[[2, 2]] = -bb[[1, 1]]; m1 = {{1/sq, 0}, {0, -sq}}; bb . m0 + m0 . Transpose[bb]

enter image description here

The third equation:

mpl = {{1/sg, 1}, {1, sg}}; Reduce[bb . mpl + mpl . Transpose[bb] == 2 w sg, Most@Flatten@bb]

enter image description here

And the forth equation:

mpl = {{1/sg, -1}, {-1, sg}}; Reduce[bb . mpl + mpl . Transpose[bb] == -2 w sg, Most@Flatten@bb]

enter image description here

Now if w= 0 and sg !=0 the third equation requests that: b12= -b11/sg, but the forth: b12= -b11/sg. This leaves only the trivial solution bb={{0,0},{0,0}}.

But if w != 0, the third equation requests sg==1 and the fourth sg == -1, therefore there is no solution in this case.

Improve this answer
$\endgroup$
1
  • $\begingroup$ i am sorry, maybe didn't express my problem clearly, $M_0,M_1,M_\pm$ and $\lambda_0,\lambda_1,\lambda_\pm$ is the result given in the paper, and now I want to get these results from the matrix equation, but I don't know how to solve them. The source of the problem is (arxiv.org/pdf/1910.00604.pdf) about how to solve the covariance matrix equation in Appendix_Dissipative dynamics. $\endgroup$ Commented Aug 6, 2022 at 9:19

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.