1
$\begingroup$

Whoever is reading this have to be patient as the code is slightly long and I have explain each section in order to explain the problem. So I want to solve the set of non-linear algebraic equation using FindRoot. Here is the first section of the code,

np = 11; zbound[\[Delta]_] := Re[z /. FindRoot[Cos[\[Delta]] Cosh[3 \[Delta]] + Sin[\[Delta]] Sinh[\[Delta]] + (z(-4\[Delta] Cos[\[Delta]] Cosh[3 \[Delta]] + Sin[\[Delta]] (Cosh[\[Delta]] - 4 \[Delta] Sinh[\[Delta]]) + Cos[\[Delta]] Sinh[3 \[Delta]]))/\[Delta] == 0, {z, 0.1}]] zvalue = Table[z[i], {i, 1, np}]; guess = Table[(-((np + 1)/2) + i)*(0.5*I)/10000, {i, 1, np}] eqn[\[Delta]_] := Table[(E^(-I*z[i]*20000) == \!\(\*UnderoverscriptBox[\(\[Product]\), \(j = 1\), \(np\)]\(If[j != i, \*FractionBox[\((I*\((\*FractionBox[\(z[i] - z[j]\), \(2\)])\) - zbound[\[Delta]])\), \((\(-I\)*\((\*FractionBox[\(z[i] - z[j]\), \(2\)])\) - zbound[\[Delta]])\)], 1]\)\)), {i, np}];

Just copy and paste the above code into Mathematica Notebook. The last line is the non-linear equation I want to solve.

eqnsol[\[Delta]_, initialvalue_] :=zvalue /.FindRoot[eqn[\[Delta]],Transpose[{zvalue, initialvalue}], MaxIterations -> 400]

This will find the solution of the equations that depends on $\delta$. With the initial value as "guess",

Block[{\[Delta] = 1.60919303}, eqnsol[\[Delta], guess]]

This will give me the solution of a particular value of $\delta$. Now, I want to evolve the solution by increasing the value of $\delta$.

\[Delta]list = SetPrecision[Range[1.60919303, 1.60919305, 10^-9], 10]; approxData = {}; Do[sol = eqnsol[\[Delta], guess]; AppendTo[approxData, sol]; guess = sol;, {\[Delta], \[Delta]list}]

This will evolve the solution by updating the guess as previous solution. I can plot the data with respect to $\delta$.

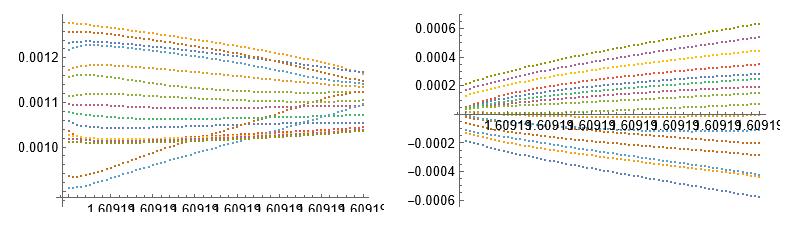
GraphicsRow[{ListPlot[Table[Transpose[{\[Delta]list, Re[approxData[[All, i]]]}], {i, 1, np}]],ListPlot[Table[Transpose[{\[Delta]list, Im[approxData[[All, i]]]}], {i, 1, np}]]}]

enter image description here

No problem till this point. Now if I want to increase the range of $\delta$,

\[Delta]list = SetPrecision[Range[1.60919303, 1.6091931, 10^-9], 10];

Running the same loop, you get error, and it spits out some junk values.

enter image description here

enter image description here

Reasoning behind it I believe is that as the solution increases, the exponent in the LHS of the equation is decreasing, and at some point it becomes smaller that the precision of the code. I tried increasing the WorkingPrecision but it didn't work.

Note: If someone is able to solve the problem, try also increasing the value of np to some odd integer to see the solution holds or not.

Improve this question
$\endgroup$
2
  • $\begingroup$ @Bill I tried that, but I am not seeing any syntax error. $\endgroup$ Commented Mar 23, 2023 at 21:19
  • 1
    $\begingroup$ It is not necessary to use a numeric technique (i.e., FindRoot) in the definition of zbound. Use zbound[\[Delta]_] = Re[SolveValues[Cos[\[Delta]] Cosh[3 \[Delta]] + Sin[\[Delta]] Sinh[\[Delta]] + (z (-4 \[Delta] Cos[\[Delta]] Cosh[3 \[Delta]] + Sin[\[Delta]] (Cosh[\[Delta]] - 4 \[Delta] Sinh[\[Delta]]) + Cos[\[Delta]] Sinh[3 \[Delta]]))/\[Delta] == 0, z][[1]]]; $\endgroup$ Commented Mar 23, 2023 at 22:20

1 Answer 1

Reset to default
3
+100
$\begingroup$

As Bob stated, can solve for $z$ explicitly in zbound (I changed the variable names to distinguish my code):

newZBound[\[Delta]_] = z /. Solve[ Cos[\[Delta]] Cosh[3 \[Delta]] + Sin[\[Delta]] Sinh[\[Delta]] + (z (-4 \[Delta] Cos[\[Delta]] \ Cosh[3 \[Delta]] + Sin[\[Delta]] (Cosh[\[Delta]] - 4 \[Delta] Sinh[\[Delta]]) + Cos[\[Delta]] Sinh[3 \[Delta]]))/\[Delta] == 0, z][[1, 1]]

Now try $np=25$:

 np = 25; newEqn[\[Delta]_] := Table[(E^(-I*z[i]*20000) == \!\( \*UnderoverscriptBox[\(\[Product]\), \(j = 1\), \(np\)]\(If[j != i, \*FractionBox[\((I*\(( \*FractionBox[\(z[i] - z[j]\), \(2\)])\) - newZBound[\[Delta]])\), \((\(-I\)*\(( \*FractionBox[\(z[i] - z[j]\), \(2\)])\) - newZBound[\[Delta]])\)], 1]\)\)), {i, np}];

Now, for the guess values you initially used a pure imaginary number and specified 0.5 which immediately drops the precision to machine precision. Running that by itself, when the number of equation increase above 11, FindRoot encounters a singular Jacobian and recommends perturbing the intitial values. So I first change 0.5 to 1/2 to force arbitrary precision and add a perturb value of 1/1000 in the guess list:

perturbVal = 1/1000; zvalue = Table[z[i], {i, 1, np}]; guess = Table[(-((np + 1)/2) + i)*(1/2*I)/10000 + perturbVal, {i, 1, np}] newEqnSol[\[Delta]_, initialvalue_] := zvalue /. FindRoot[newEqn[\[Delta]], Transpose[{zvalue, initialvalue}], MaxIterations -> 400]

Now increase the range of $\delta$ and plot the resutls:

\[Delta]list = SetPrecision[Range[1.60919303, 1.6091931, 10^-9], 10] approxData = {}; Do[sol = newEqnSol[\[Delta], guess]; AppendTo[approxData, sol]; guess = sol;, {\[Delta], \[Delta]list}] GraphicsRow[{ListPlot[ Table[Transpose[{\[Delta]list, Re[approxData[[All, i]]]}], {i, 1, np}], PlotStyle -> PointSize[0.0075]], ListPlot[ Table[Transpose[{\[Delta]list, Im[approxData[[All, i]]]}], {i, 1, np}], PlotStyle -> PointSize[0.0075]]}]

enter image description here

Improve this answer
$\endgroup$
3
  • $\begingroup$ What version do you run? $\endgroup$ Commented Mar 28, 2023 at 16:04
  • $\begingroup$ @josh Awesome solution. However, I don't think this is correct solutions. Yes, the numerical code is running, but if you notice, the sum of all the z's have to be zero. That's why I took purely imaginary guess. This can be checked by taking np=3 and just multiply three equations. You will get $e^{i(z_1+z_2+z_3)*(20000)}=1$. Anyway, this is a good starting point for me to change the guess values and see if I get near my solutions. $\endgroup$ Commented Mar 28, 2023 at 17:32
  • $\begingroup$ @Alex Trounev: I'm running 13.2 $\endgroup$ Commented Mar 28, 2023 at 17:38

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.