0
$\begingroup$

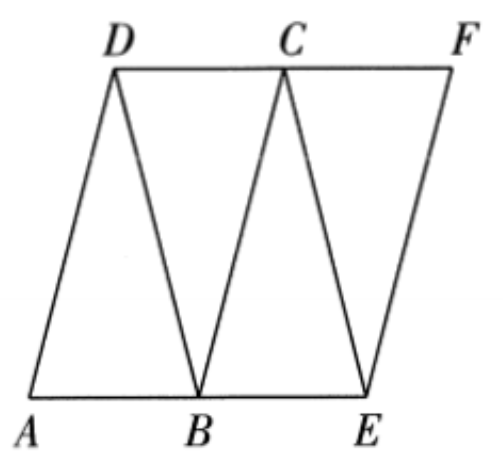
enter image description here

A planar expansion diagram of a tetrahedron ABCD is shown in the above figure, where the quadrilateral AEFD has a diamond with a side length of 2Sqrt 2, B and C are the midpoints of AE and FD, respectively, and BD=2Sqrt 2

Clear["Global`*"]; a = {0, 0}; b = {Sqrt[2], 0}; e = {2 Sqrt[2], 0}; d = {Sqrt[2]/2, Sqrt[30]/2}; c = {3 Sqrt[2]/2, Sqrt[30]/2}; f = {5 Sqrt[2]/2, Sqrt[30]/2}; rl = Line[{{a, b}, {b, e}, {e, f}, {f, c}, {c, d}, {a, d}, {b, d}, {b, c}, {c, e}}]; labels = {Text[Style[A, 12, FontFamily -> "Times"], a, {1, 1}], Text[Style[B, 12, FontFamily -> "Times"], b, {1, 1}], Text[Style[C, 12, FontFamily -> "Times"], c, {-2, -1}], Text[Style[D, 12, FontFamily -> "Times"], d, {3, 0}], Text[Style[E, 12, FontFamily -> "Times"], e, {-1, 1}], Text[Style[F, 12, FontFamily -> "Times"], f, {0, -1}]}; Graphics[{rl, labels}]

Can you draw its planar shape and find a way to convert it into a spatial tetrahedron?

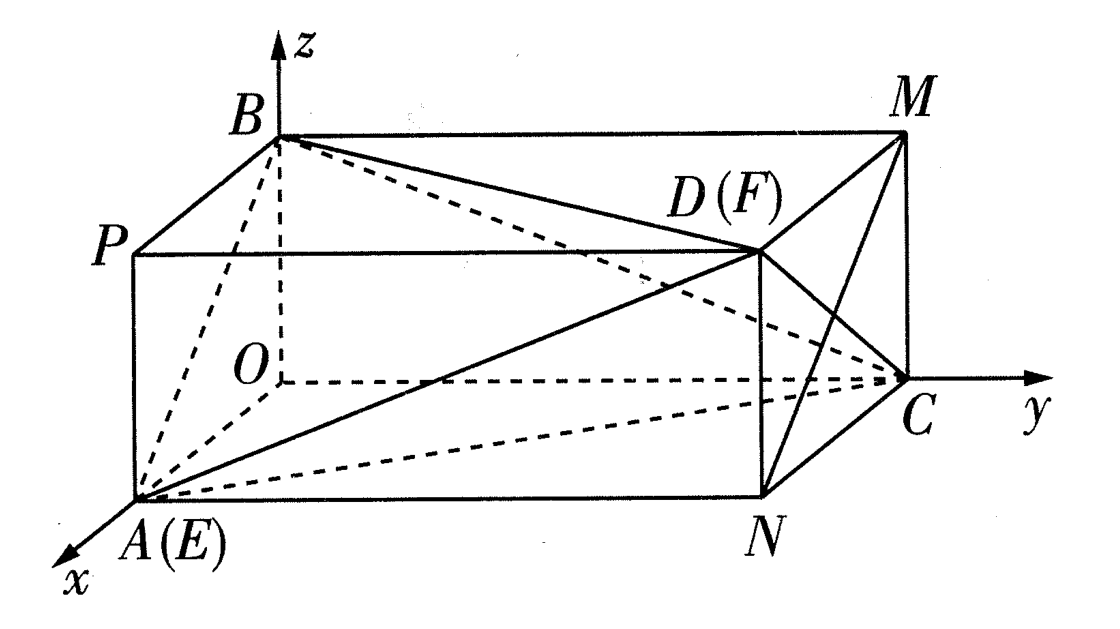
enter image description here

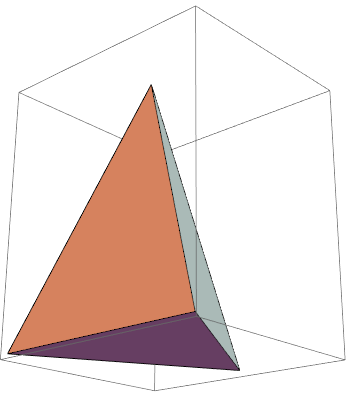
This flat unfolding diagram is restored to a spatial geometry, which is a tetrahedron with equal length relative to its edges, as shown in the following figure,The tetrahedron in the middle of the cuboid,The length, width, and height of the outer cuboid are:Sqrt[7], 1, 1,Figure A (E) CD (F) B is the final desired result:

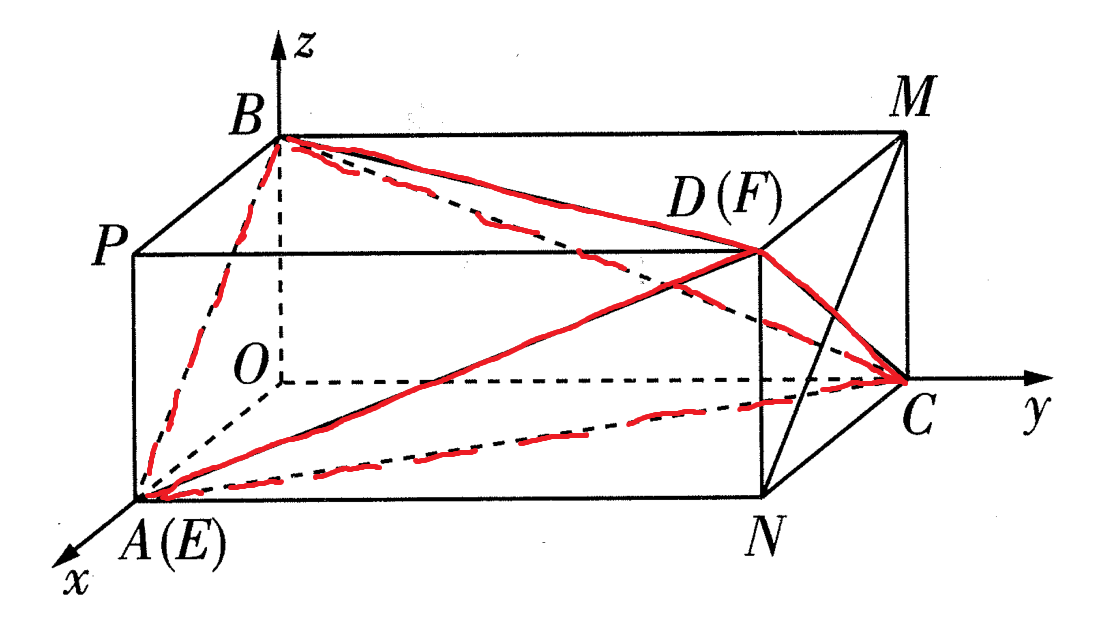
enter image description here

To be more intuitive, the spatial geometry marked in red in the following image is the final shape.

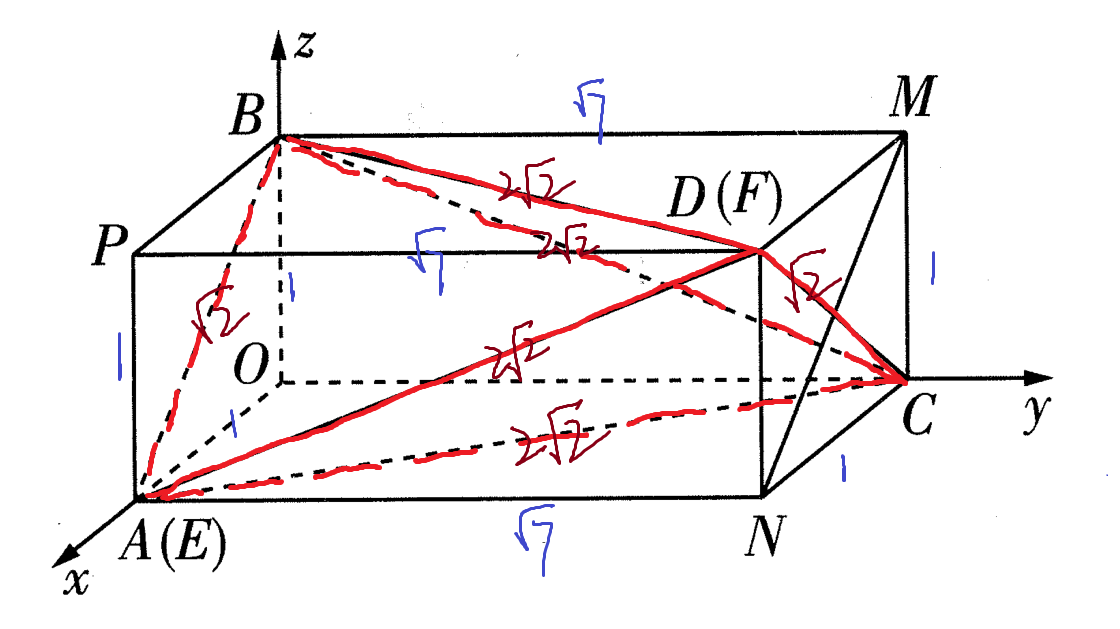
enter image description here

The relationship between the length, width, and height of a cuboid and the edge length of a tetrahedron is shown in the figure below, and the quantity of each edge length has been identified. Prove that the red part of the tetrahedron is the desired one.

enter image description here

Improve this question
$\endgroup$
4
  • 1
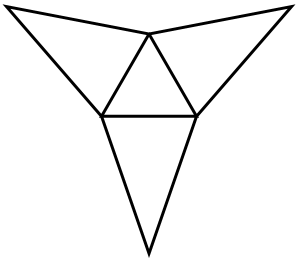
    $\begingroup$ PolyhedronData["Tetrahedron", "Net"] doesn't match with the OP. $\endgroup$ Commented Dec 7, 2023 at 15:21
  • $\begingroup$ related: Faces and NetFaces relation in polyhedron $\endgroup$ Commented Dec 8, 2023 at 7:50
  • $\begingroup$ @Syed The obtained graphics and results are different $\endgroup$ Commented Dec 9, 2023 at 0:21
  • $\begingroup$ Mathworld page suggests that there can be two (types) cuts for a tetrahedron, so your figure may still be foldable. $\endgroup$ Commented Dec 9, 2023 at 4:43

1 Answer 1

Reset to default
2
$\begingroup$

There are four small sides, a triangle of this size is missing. It has to be placed in the center and for a general elonged pyramid, the angles at its verices do not produce straight outer lines. If you cut off the bottom equal sided triangle, its appended on one of the shorter side. Try eg

With[{a=2Pi/3}, Graphics3D[Tetrahedron[ {{0,0,2},{0,1,0},{Sin[a],Cos[a],0},{Sin[-a],Cos[-a],0}}]]]

Tetrahedron

I looked for a net word, without success, works only with names. So done by hand, not exactly solving for the diagonal lengths

 With[{a = 2 Pi/3, b = 2 \[Pi]/6, c = -2 \[Pi]/6 }, Graphics[{Thickness[0.01], Line[{{0, 1}, {Sin[a], Cos[a]}, {Sin[-a], Cos[-a]}, {0, 1}, 3 {Sin[b], Cos[b]}, {Sin[a], Cos[a]}, {0, -3}, {Sin[-a], Cos[-a]}, 3 {Sin[c], Cos[c]}, {0, 1}}]}] ]

Net of Tetrahedron

Improve this answer
$\endgroup$
0

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.