4
$\begingroup$

For some purposes I need detailed mesh models of 2D and 3D shapes. No problem with 2D, so for Rectangle[] we get for example

DiscretizeRegion[Rectangle[], MaxCellMeasure -> {"Length" -> #}] & /@ {0.2, 0.1}

enter image description here
For Sphere[] it's OK too:
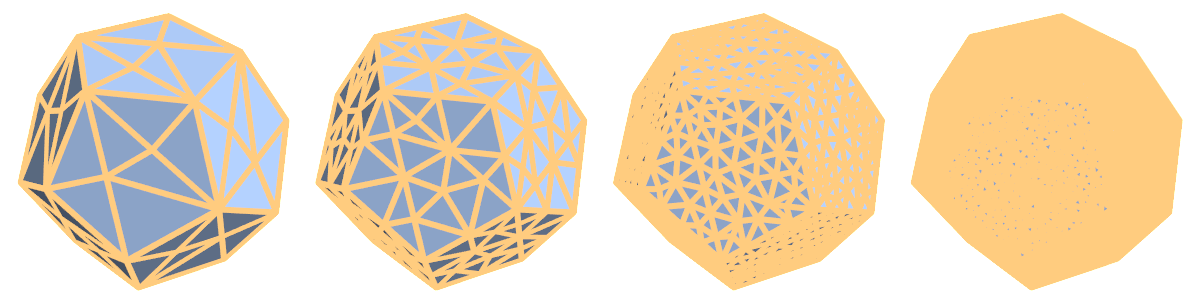
enter image description here
But for Dodecahedron[] result is undesirable:
enter image description here
I need all the faces of dodecahedron to be disсretized detailed, just as rectangle above!
I’ve tried every way: MaxCellMeasure, BoundaryDiscretizeRegion, MeshRefinementFunction etc, all the same ((

Improve this question
$\endgroup$

1 Answer 1

Reset to default
6
$\begingroup$

Edit

I found that "Length" -> .2 work when we use PolyhedronData["Dodecahedron", "BoundaryMeshRegion"] instead of Dodecahedron[]. Of course, PolyhedronData["Dodecahedron", "MeshRegion"] still need to use "Volume".

HighlightMesh[ DiscretizeRegion[ PolyhedronData["Dodecahedron", "BoundaryMeshRegion"], MaxCellMeasure -> {"Length" -> .2}, AccuracyGoal -> 1], 1]

enter image description here

  • Add the comment of @Syed
HighlightMesh[ BoundaryDiscretizeRegion[Dodecahedron[], MaxCellMeasure -> {"Length" -> #}], 1] & /@ {1, 1/2, 1/4, 1/8}

enter image description here

Original

Set AccuracyGoal -> 5 and "Volume".

HighlightMesh[ DiscretizeRegion[Dodecahedron[], MaxCellMeasure -> {"Volume" -> .002}, AccuracyGoal -> 5], 1]

enter image description here

Improve this answer
$\endgroup$
6
  • $\begingroup$ Volume /)_-) Many thanks! $\endgroup$ Commented Feb 12, 2024 at 11:16
  • $\begingroup$ I would hae used DiscretizeRegion[Dodecahedron[], MaxCellMeasure -> {1 -> 0.05}]. But surprisingly, it just ignores the edge length constraint MaxCellMeasure ->{1 -> 0.05}. Maybe it is worth reporting it as a bug? $\endgroup$ Commented Feb 12, 2024 at 15:18
  • 1
    $\begingroup$ @HenrikSchumacher, yes, anyway the need to use Volume keyword for facet mesh looks strange $\endgroup$ Commented Feb 12, 2024 at 15:27
  • $\begingroup$ I think you should really write Wolfram Support about this. They probably won't change this soon; but it is some feedback that they might appreciate. $\endgroup$ Commented Feb 12, 2024 at 15:29
  • 1
    $\begingroup$ BoundaryDiscretizeRegion[Dodecahedron[], MaxCellMeasure -> {2 -> #}] & /@ {1, 1/2, 1/4, 1/8} $\endgroup$ Commented Feb 12, 2024 at 16:21

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.