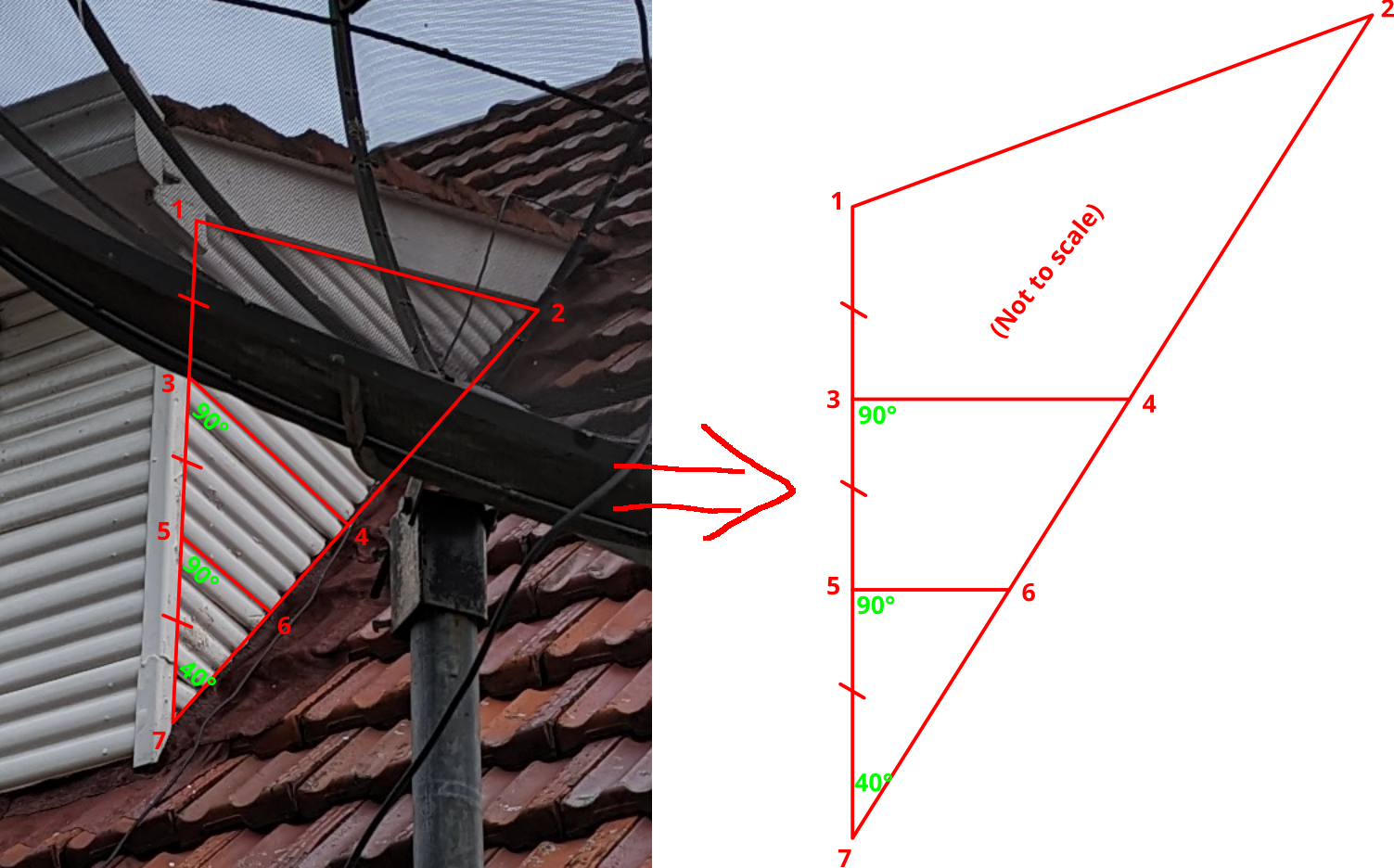
I have taken a photo (with a rectilinear lens) of a house's outside wall that sits on top a roof, from which I wish to take measurements from. However, to do so I would need to correct the perspective so the wall appears parallel to the image
To assist with this, I have some known properties of the wall, which I have labelled above:
- ∠172 = 40° (the roof is 40° from the vertical)
- ∠756 = 90°, ∠734 = 90° (the white "slats" are horizontal)
- Points 1,3,5,7 are colinear, and divide the segment into thirds (the slats have identical heights)
- Point 6 is the midpoint of points 4 and 7 (similar triangles)
- Points 2,4,6,7 are colinear
First of all, lets make some definitions:
$$ \begin{align} n &= \textrm{Point number as indicated on the diagram} \\ \textrm{image}[n] &= \mathbb{R}^2 \textrm{ coordinates of points in the original (left) image} \\ \textrm{error}[n] &= \mathbb{R}^2 \textrm{ measurement error of the above coordinates} \\ \textrm{base}[n] &= \mathbb{R}^2 \textrm{ coordinates of points in the projected (right) image} \\ \textrm{projection} &= \begin{pmatrix} p[1,1] & p[1,2] & p[1,3] \\ p[2,1] & p[2,2] & p[2,3] \\ p[3,1] & p[3,2] & 1 \end{pmatrix} \textrm{ arbitrary projection using }\mathbb{R}^3\textrm{ homogeneous coordinates} \\ \textrm{cosAngle}(\textrm{a, b, c}) &= \frac{(\textrm{a} - \textrm{b})\cdot(\textrm{c} - \textrm{b})}{|\textrm{a} - \textrm{b}| |\textrm{c} - \textrm{b}|} \textrm{ cosine of angle ∠abc} \end{align} $$
So this problem simply becomes an optimisation problem where we want to minimise the $\textrm{error}[n]$ terms, and then extract the $\textrm{projection}$ or $\textrm{base}$ terms, under the following constraints:
$$ \begin{align} & \textrm{(base is a perspective transform of image)} \\ \textrm{base}[n] &= \frac{\textrm{projection} \begin{pmatrix}\textrm{image}[n] + \textrm{error}[n] \\ 1\end{pmatrix}}{\begin{pmatrix}p[3,1] \\ p[3,2] \\ 1\end{pmatrix} \cdot \begin{pmatrix}\textrm{image}[n] + \textrm{error}[n] \\ 1\end{pmatrix}} \\ & \textrm{(arbitrary reference coordinates to absorb rotation, scale, and translation degrees of freedom)} \\ \textrm{base}[7] &= \begin{pmatrix}0 \\ 0\end{pmatrix} \\ \textrm{base}[1] &= \begin{pmatrix}0 \\ -1\end{pmatrix} \\ & \textrm{(colinearity and proportionality)} \\ \textrm{base}[5] &= \frac{1}{3} \textrm{base}[1] \\ \textrm{base}[3] &= \frac{2}{3} \textrm{base}[1] \\ \textrm{base}[6] &= \frac{1}{2} \textrm{base}[4] \\ \cos 0 &= \textrm{cosAngle}(\textrm{base}[4], \textrm{base}[7], \textrm{base}[2]) \\ & \textrm{(angles)} \\ \cos 40° &= \textrm{cosAngle}(\textrm{base}[1], \textrm{base}[7], \textrm{base}[2]) \\ \cos 90° &= \textrm{cosAngle}(\textrm{base}[7], \textrm{base}[5], \textrm{base}[6]) \\ \cos 90° &= \textrm{cosAngle}(\textrm{base}[7], \textrm{base}[3], \textrm{base}[4]) \end{align} $$
Here is my attempt to perform least squares minimisation with Mathematica 12.0
image = { {2871.87,1626.04}, {3240.15,1722.65}, {2863.93,1794.74}, {3035.29,1953.99}, {2855.83,1966.57}, {2951.74,2048.33}, {2846.37,2167.32} }; error = Table[{ex[n], ey[n]}, {n, 1, 7}]; base = Table[{bx[n], by[n]}, {n, 1, 7}]; projection = Table[If[x == 3 && y == 3, 1, p[x,y]], {x, 1, 3}, {y, 1, 3}]; cosAngle[a_, b_, c_] := (a-b).(c-b) / Norm[a-b] / Norm[c-b]; constraints = { ((projection.Join[#, {1}])/(projection[[3]].Join[#, {1}]) & /@ (image + error))[[All, 1;;2]] == base, (*arbitrary reference coordinates*) base[[7]] == {0, 0}, base[[1]] == {0, -1}, (*colinearity and proportionality*) base[[5]] == base[[1]] / 3, base[[3]] == 2 base[[1]] / 3, base[[6]] == base[[4]] / 2, cosAngle[base[[4]],base[[7]],base[[2]]] == Cos[0], (*angles*) cosAngle[base[[1]],base[[7]],base[[2]]] == Cos[40 Degree], cosAngle[base[[7]],base[[5]],base[[6]]] == Cos[90 Degree], cosAngle[base[[7]],base[[3]],base[[4]]] == Cos[90 Degree] }; NMinimize[{ Total[#.# & /@ error], And@@constraints }, Select[Flatten@Join[projection, error, base], !SameQ[#, 1] &]] But Mathematica is unable to find a solution, erroring with NMinimize::nosat: Obtained solution does not satisfy the following constraints... with a list of 13 constraints afterwards
Am I approaching this problem correctly? Have I made some incorrect assumptions?
Why is Mathematica unable to find a solution?
