5
$\begingroup$

This problem from Ordinary Differential Equations, By Tenenbaum and Pollard. Dover, NY 1963, Chapter 8. Special second order equations. Lesson 35. Independent variable x absent, Exercise 35.18, page 504.

Maple solves it but Mathematica says

DSolve::bvfail: For some branches of the general solution, unable to solve the conditions.

Verified Maple solution is correct.

Any workaround or why Mathematica does not solve it?

ClearAll[y, x]; ode = y''[x] == 2*y[x]*y'[x] ic = {y[0] == 1, y'[0] == 2} DSolve[{ode, ic}, y[x], x] (* {} *)

Maple:

ode:=diff(y(x),x$2)=2*y(x)*diff(y(x),x); ic:=y(0)=1,D(y)(0)=2; dsolve([ode,ic])

$$ y \left(x \right) = \tan \left(x +\frac{\pi}{4}\right) $$

Verified solution is correct

sol=y->Function[{x},Tan[x+Pi/4]] {ode,ic}/.sol

gives

(* {True, {True, True}} *)

Maple has also step-by-step solver. These are the steps it did (can't post Latex, but only screen shot). The problems seems to be in how Maple solved for the constants of integration vs. Mathematica? Because Mathematica has no problem solving the ODE with no IC:

 DSolve[ode, y[x], x]

$$ \left\{\left\{y(x)\to \sqrt{c_1} \tan \left(\sqrt{c_1} x+\sqrt{c_1} c_2\right)\right\}\right\} $$

Which is the similar but not exactly the same as Maple with no ic (Mathematica could have re-written the constants to get rid of the sqrt in them)

 dsolve(ode)

$$ y \left(x \right) = \frac{\tan \left(\frac{c_{2} +x}{c_{1}}\right)}{c_{1}} $$

So that is why I think the problem is how to solve for the constants from the general solution. (Mathematica also says that in its message unable to solve the conditions. )

Here are Maple's step-by-step

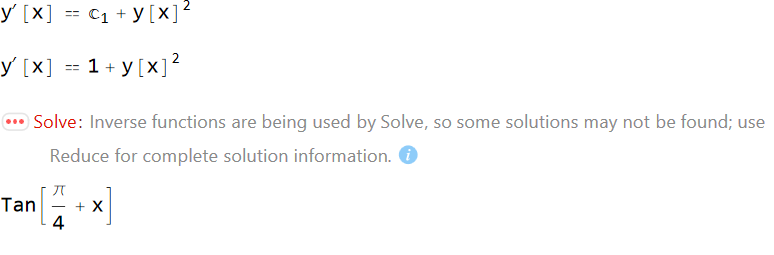
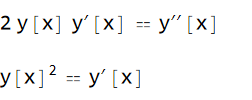
enter image description here

enter image description here

enter image description here

Improve this question
$\endgroup$
1
  • 1
    $\begingroup$ There is no unique solution. Use Reduce[ic /. DSolve[ode, y, x][[1]], {C[1], C[2]}] to observe all branches. $\endgroup$ Commented May 9, 2024 at 3:18

2 Answers 2

Reset to default
5
$\begingroup$

Using the hack by @MichaelE2, we get the following workaround:

(*https://mathematica.stackexchange.com/a/63676*) Internal`InheritedBlock[{Solve}, Unprotect[Solve]; Solve[eq_, v_, opts___] /; ! TrueQ[$in] := Block[{$in = True, $res1, $res2}, Solve[eq, v, Reals, Method -> Reduce, opts]]; Protect[Solve]; ode = y''[x] == 2*y[x]*y'[x]; ic = {y[0] == 1, y'[0] == 2}; DSolve[{ode, ic}, y[x], x] // Simplify ] (* {{y[x] -> ConditionalExpression[ Tan[\[Pi]/4 + x], -((3 \[Pi])/4) < x < \[Pi]/4]}} *)

It seems to me that if $y=\tan(\pi/4 + x)$ is solution, then so are $y = \tan(5\pi/4 + x)$, $y = \tan(9\pi/4 + x)$, and so on. That may have something to do with DSolve[] obtaining the (complete?) solution to the IVP. The Maple solution, as well as the workaround solution presented in this answer, seems more like a FindInstance solution than the complete solution. [Update, after some catch-up sleep: Actually half of the struck-out sentence is nonsense, and half is pertinent. Since we have identically $\tan(pi/4 + x) = \tan(5\pi/4 + x) = \cdots$, the Maple and above solutions are complete. OTOH, the code below shows that the pseudo-multiplicity is something to be dealt with.]

Note using Solve on the IC and DSolve for the general solution shows the fake multiplicity:

DSolve[{ode(*,ic*)}, y, x] Solve[ic /. First[%], {C[1], C[2]}] // Simplify (* {{y -> Function[{x}, Sqrt[C[1]] Tan[x Sqrt[C[1]] + Sqrt[C[1]] C[2]]]}} {{C[1] -> ConditionalExpression[1, Element[C[3], Integers]], C[2] -> ConditionalExpression[ (1/4)*Pi*(1 + 8*C[3]), Element[C[3], Integers]]}, {C[1] -> ConditionalExpression[1, Element[C[3], Integers]], C[2] -> ConditionalExpression[ (1/4)*Pi*(-3 + 8*C[3]), Element[C[3], Integers]]}} *)
Improve this answer
$\endgroup$
2
  • $\begingroup$ It is a nice approach (+1). What version do you run? $\endgroup$ Commented May 9, 2024 at 11:09
  • $\begingroup$ @AlexTrounev Thanks and sorry for the late reply. I went traveling right after this and lost track of messages. $\endgroup$ Commented Jun 21, 2024 at 15:04
3
$\begingroup$

I appreciate that the aim of the question is to automate identifying that the ODE is equivalent to $y'(x)=y(x)^2+c$, where $c$ is a constant:

The desired result can be derived:

sys = y'[x] == y[x]^2 + C[1] eqn = sys /. x -> 0; de = sys /. ToRules[Reduce[{eqn, y[0] == 1, y'[0] == 2}, C[1]]] y[x] /. DSolve[{de, y[0] == 1, y'[0] == 2}, y[x], x][[1]]

enter image description here

The equivalence:

p1 = D[y[x]^2, x] == D[y'[x], x] p2 = ApplySides[Integrate[#, x] &, p1]

Unfortunately, using GeneratedParameters yields the same constant on both sides.

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.