0
$\begingroup$

How can I simplify this formula.

$$ \frac{V_x - V_{\text{out}}}{s L} - \frac{V_{\text{out}}}{R_L} - V_{\text{out}}s C_1 = V_x g_m \tag{1} $$

$$ \frac{V_x - V_{\text{out}}}{s L} + V_x s C_2 =0 \tag{2} $$

We can find $V_x = \frac{V_{out}} {1 + s^2 C_2 L}$ from (2).

Based on (1), we have $$- V_{out} (\frac{1} {s L} + \frac{1} {R_L} + s C_1) = V_x \biggl(g_m - \frac{1} {s L}\biggl)$$

substitute $\frac{V_{out}} {1 + s^2 C_2 L}$ for $V_x$

$$- V_{out} (\frac{1} {s L} +\frac{1} {R_L} + s C_1) = \frac{V_{out}} {1 + s^2 C_2 L} \biggl(g_m - \frac{1} {s L}\biggl)$$

$$- (\frac{1} {s L} + \frac{1} {R_L} + s C_1) = \frac{1} {1 + s^2 C_2 L} \biggl(g_m - \frac{1} {s L}\biggl)$$

$$(\frac{1} {s L} + \frac{1} {R_L} + s C_1) (1 + s^2 C_2 L) = \biggl(-g_m + \frac{1} {s L}\biggl)$$

$$\frac{1} {s L} + s C_1 + s C_2 + \frac{1 + s^2 C_2 L} {R_L} + s^3 C_1 C_2 L = \biggl(-g_m + \frac{1} {s L}\biggl)$$

$$ s (C_1 + C_2) + \frac{1 + s^2 C_2 L} {R_L} + s^3 C_1 C_2 L = -g_m $$

because $ s \to j \omega$

$$ j \omega (C_1 + C_2) + \frac{1 - \omega^2 C_2 L} {R_L} - j \omega^3 C_1 C_2 L = -g_m $$

$$ g_m + \frac{1 - \omega^2 C_2 L} {R_L} - j \omega^3 C_1 C_2 L + j \omega (C_1 + C_2) =0 $$

$$ g_m + \frac{1 - \omega^2 C_2 L} {R_L} + j \omega \biggl( (C_1 + C_2) - \omega^2 C_1 C_2 L \biggl) =0 $$

$$ \Rightarrow g_m + \frac{1 - \omega^2 C_2 L} {R_L} =0 $$

$$ \Rightarrow \omega \biggl( (C_1 + C_2) - \omega^2 C_1 C_2 L \biggl) = 0 $$

Here is what I tried to simplify this.

eq1 = (Vx - Vout)/(s L) - Vout/RL - Vout/(s C1) == Vx gm /. s -> I w; sols = Solve[eq1, Vx] eq2 = (Vx - Vout)/(s L) + Vx s C2 /. s -> I w; rect = eq2 /. sols[[1]] final = rect/Vout; ComplexExpand[ReIm[final]] // Simplify

However, I got this in 12.0

{-(((C1 + C1 gm RL + gm L RL) (-1 + C2 L w^2))/( C1 RL (1 + gm^2 L^2 w^2))), ( C1 gm L w^2 (1 - C2 L w^2) + RL (-1 + C2 L w^2 + C1 (C2 + gm^2 L) w^2))/( C1 RL w (1 + gm^2 L^2 w^2))}

enter image description here

The answer from Mathematica is different from $g_m + \frac{1 - \omega^2 C_2 L} {R_L} (real) $ and $\omega \biggl( (C_1 + C_2) - \omega^2 C_1 C_2 L \biggl) (imaginary)$

Improve this question
$\endgroup$
6
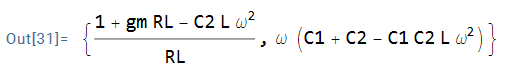
  • $\begingroup$ Your code outputs {-(((C1+C1 gm RL+gm L RL) (-1+C2 L w^2))/(C1 RL (1+gm^2 L^2 w^2))),(C1 gm L w^2 (1-C2 L w^2)+RL (-1+C2 L w^2+C1 (C2+gm^2 L) w^2))/(C1 RL w (1+gm^2 L^2 w^2))}. in 14.1 on Windows. What do you dislike about it? $\endgroup$ Commented Oct 25, 2024 at 12:23
  • $\begingroup$ @user64494 It's not the same as hand calculation $\endgroup$ Commented Oct 25, 2024 at 12:24
  • 1
    $\begingroup$ Not seeing that "hand calculation", one can say nothing. $\endgroup$ Commented Oct 25, 2024 at 12:26
  • $\begingroup$ @user64494 I have edited it for better reading $\endgroup$ Commented Oct 25, 2024 at 12:36
  • $\begingroup$ I believe the beginning of your hand calculations have a couple errors, one minor, one significant. The solution for Vx is derived from Eq 2, not 1. The next equation is derived from Eq 1, not 2 and the term sC1 should be 1/sC1. $\endgroup$ Commented Oct 25, 2024 at 16:06

1 Answer 1

Reset to default
4
$\begingroup$

This works for me in version 14.1:

eq1 = (Vx - Vout)/(s L) - Vout/RL - s C1 Vout == Vx gm; eq2 = (Vx - Vout)/(s L) + Vx s C2 == 0; eq3 = Eliminate[{eq1, eq2, Vout != 0}, {Vout, Vx}][[1, 1]] // Simplify (* Out *) gm + (1 + C2 L s^2)/RL + s (C1 + C2 + C1 C2 L s^2) == 0 ComplexExpand[ReIm[eq3 /. s -> I \[Omega]]]

Final Output

Improve this answer
$\endgroup$
2
  • $\begingroup$ Can we use Assumptions for Vout != 0? $\endgroup$ Commented Oct 25, 2024 at 19:03
  • $\begingroup$ @kile, Simplify takes assumptions, so you can use Simplify[Eliminate[{eq1, eq2}, Vx], Vout != 0] in the expression for eq3. That will generate a result with a slightly different form wrt RL, but should be equivalent. $\endgroup$ Commented Oct 25, 2024 at 19:35

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.