3
$\begingroup$

I must be misunderstanding things but RegionBoundary isn't doing what I naively expect it to do.

In the following code I find the points of an integer lattice that fall within an ImplicitRegion of a quarter circle and the coordinate axes.

ddp[equation_, bnd_] := Module[{eqn = equation, bound = bnd, \[ScriptCapitalR], lattice, pts, pts2, pts3, number}, \[ScriptCapitalR] = ImplicitRegion[ eqn && 0 < x <= bound + 1 && 0 < y <= bound + 1, {x, y}]; lattice = Tuples@Replace[ CoordinateBounds[\[ScriptCapitalR]], {p_, q_} :> Range[Floor[p], Ceiling[q]], {1}]; pts = Point@Select[lattice, RegionMember[\[ScriptCapitalR]]]; pts2 = Point@Select[lattice, #[[1]]^2 + #[[2]]^2 == 100 &]; pts3 = Point@Select[lattice, RegionMember[RegionBoundary[\[ScriptCapitalR]]]]; Print[pts2]; Print[pts3]; number = RegionMeasure[pts]; {number, Show[RegionPlot[\[ScriptCapitalR], PlotPoints -> 2, MaxRecursion -> 1], Graphics[{Red, PointSize[.015], pts}], Graphics[{Black, PointSize[.03], pts2}], Frame -> True]} ]

The defined function is called by

lim = 100; res = ddp[x^2 + y^2 <= lim, lim]; res[[1]] res[[2]] (* Point[{{0,10},{6,8},{8,6},{10,0}}] *) (* Point[{}] *) (* 69 *) (* Graphic displayed (but I do not know how to show that on here) *)

Now finding the lattice points in the defined region works (pts in the function). But it will not find the lattice points that lie on the region boundary alone (pts3 in the function). Obviously I can find the lattice points on the boundary using the explicit formula in the pts2 calculation.

My question is: Why doesn't using RegionMember on the RegionBoundary find these points that lie on the boundary? And is there a way of using RegionBoundary for this?

Improve this question
$\endgroup$
5
  • $\begingroup$ This looks like an bug to me. I would ask Wolfram about this. $\endgroup$ Commented Nov 2, 2024 at 10:15
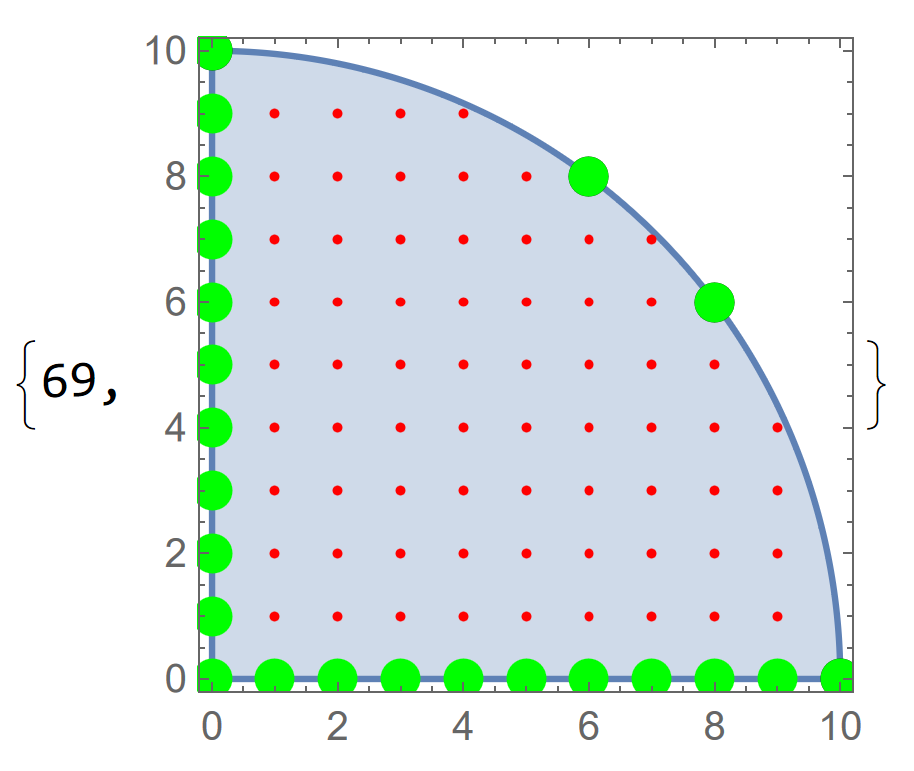
  • $\begingroup$ Please provide your version number. 13.3,14.0 and 14.1 get the correct result . Point[{{0,0},{0,1},{0,2},{0,3},{0,4},{0,5},{0,6},{0,7},{0,8},{0,9},{0,10},{1,0},{2,0},{3,0},{4,0},{5,0},{6,0},{7,0},{8,0},{9,0},{10,0}}] $\endgroup$ Commented Nov 2, 2024 at 11:16
  • $\begingroup$ 11.3, 13.3.1, 14.0,14.1 work fine, but 12.2 and 12.3 not. $\endgroup$ Commented Nov 2, 2024 at 11:32
  • $\begingroup$ @cvgtm My version is 13.1.0.0 - I do have 13.3 on another machine - I'll check. I do know the problem is with the ImplicitRegion including the inequalities. $\endgroup$ Commented Nov 2, 2024 at 11:32
  • $\begingroup$ @cvgmt I just noticed - your list is NOT including the points {6,8} and {8,6} which are the points I am interesting in finding. It is obviously ignoring the boundary of the circular arc. $\endgroup$ Commented Nov 2, 2024 at 11:37

1 Answer 1

Reset to default
3
$\begingroup$
  • SignedRegionDistance equal to 0 can get the boundary points.
pts3 = Point@ Select[lattice, SignedRegionDistance[ℛ, #] == 0 &];
  • The code work for version 12.2 to 14.1.
Clear["Global`*"]; lim = 100; bound = lim; eqn = x^2 + y^2 <= lim; ℛ = ImplicitRegion[ eqn && 0 < x <= bound + 1 && 0 < y <= bound + 1, {x, y}]; lattice = Tuples@Replace[ CoordinateBounds[ℛ], {p_, q_} :> Range[Floor[p], Ceiling[q]], {1}]; pts = Point@Select[lattice, RegionMember[ℛ]]; pts2 = Point@Select[lattice, #[[1]]^2 + #[[2]]^2 == 100 &]; pts3 = Point@ Select[lattice, SignedRegionDistance[ℛ, #] == 0 &]; Print[pts2]; Print[pts3]; number = RegionMeasure[pts]; {number, Show[ RegionPlot[ℛ, PlotPoints -> 2, MaxRecursion -> 1], Graphics[{Red, PointSize[.015], pts}], Graphics[{Black, AbsolutePointSize[10], pts2, Green, pts3}], Frame -> True]}

enter image description here

Improve this answer
$\endgroup$
3
  • $\begingroup$ You beat me to it - I was about to try something like that - but have you any idea why RegionBoundary is having issues? $\endgroup$ Commented Nov 2, 2024 at 11:59
  • $\begingroup$ @ngc5139 It is a bug since your code can get all the 23 points in version 11.3 , but only get 21 points in version 13.3.1, 14.0 and 14.1. $\endgroup$ Commented Nov 2, 2024 at 12:05
  • $\begingroup$ Yeah, I think that is the issue. If I make the region a complete circle then it finds the points {-8,-6} etc. The issue is it can't handle the inequalities x>=0 and y>=0 - if I remove those and thus have the full circle it finds them without resorting to the SignedRegionDistance workaround. $\endgroup$ Commented Nov 2, 2024 at 12:25

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.