6
$\begingroup$

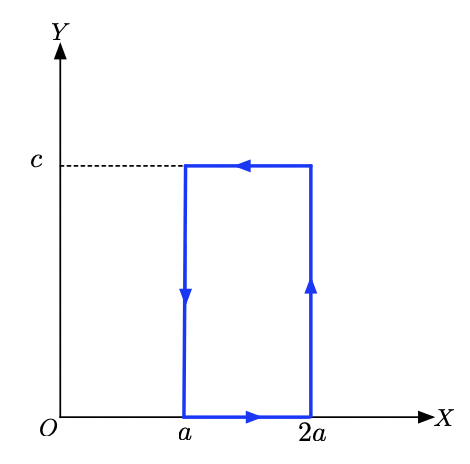
Discrepancy between LineIntegrate and SurfaceIntegrate Results in Stokes’ Theorem Verification

I’m working on an exercise in Mathematica to verify Stokes’ theorem for the 2D vector field

$$ \mathbf{A}(x,y) = A_0 (y^2, -x^2) $$

over a rectangular region defined by $ x \in [a, 2a] $ and $ y \in [0, c] $. I calculate the circulation along the boundary using LineIntegrate and get

$$ -A_0\, a\, c\,(3a+c) $$

However, when I compute the curl with

Curl[A, {x, y}]

(which returns $-2A_0\,x - 2A_0\,y$) and integrate it over the rectangle using SurfaceIntegrate, I obtain

$$ -2 A_0 (a+c)(3a+c) $$

which differs by an extra factor.

Below is the code snippet that reproduces the issue:

Clear[A0, x, y, a, c, ℛ] (* Define the vector field *) A = A0 { y^2, -x^2 } (* Out: {A0 y^2, -A0 x^2} *) (* Compute line integrals along each segment of the rectangle *) path1 = LineIntegrate[A, {x, y} ∈ Line[{{a, 0}, {2 a, 0}}]] (* Out: 0 *) path2 = LineIntegrate[A, {x, y} ∈ Line[{{2 a, 0}, {2 a, c}}]] (* Out: -4 a^2 A0 c *) path3 = LineIntegrate[A, {x, y} ∈ Line[{{2 a, c}, {a, c}}]] (* Out: -a A0 c^2 *) path4 = LineIntegrate[A, {x, y} ∈ Line[{{a, c}, {a, 0}}]] (* Out: a^2 A0 c *) (* Sum of the line integrals *) totalLine = Simplify[path1 + path2 + path3 + path4] (* Out: -a A0 c (3a + c) *) (* Compute the curl *) curlA = Curl[A, {x, y}] (* Out: -2 A0 x - 2 A0 y *) (* Define the rectangular region *) ℛ = Rectangle[{a, 0}, {2 a, c}]; (* Integrate the curl over the rectangle *) totalSurface = SurfaceIntegrate[curlA, {x, y} ∈ ℛ] // Simplify[#, Assumptions -> {a > 0, c > 0}] & (* Out: -2 A0 (a + c) (3 a + c) *)

I would expect both methods to yield the same result according to Stokes’ theorem. Has anyone seen a similar discrepancy or can explain why the surface integral gives an extra factor? Could there be a nuance with how Curl or SurfaceIntegrate handles 2D regions in Mathematica?

Any insights or suggestions would be greatly appreciated.

Here’s the geometric region for reference:
enter image description here

Improve this question
$\endgroup$

2 Answers 2

Reset to default
3
$\begingroup$

There seems somethin wrong with SurfaceIntegrate. Consider the area of a unit rectangle:

SurfaceIntegrate[1, {x, y} \[Element] Rectangle[{0, 0}, {1, 1}]] 4

Now, your case. Calculate the integral "by hand", using ordinary integration:

Integrate[-2 A0 x - 2 A0 y, {x, a, 2 a}, {y, 0, c}] // Simplify -a A0 c (3 a + c)

This gives the expected result.

Addendum

I asked Wolfram about this and here is their response:

"In this particular case, SurfaceIntegrate is behaving correctly. In 2D, the surface measure of a region corresponds to its perimeter, which is why the result is 4 for a unit rectangle."

First I did not understand this, but after studying the help I think I can now make sense of this. SurfaceIntegrate is not doing what we thought. The key sentence form the help is:

"Any n-1 dimensional RegionQ object in [DoubleStruckCapitalR]^n can be used for the surface."

I interpret this as: if you specify a n-dimensional region, then the integral is taken over the n-1 dimensional surface of this region.

Considering my example of the unit rectangle: if we specify a very thin cuboid (3D) the integral is then mainly taken over the top and bottom sides and we expect a result of 2:

SurfaceIntegrate[1, {x, y, z} \[Element] Cuboid[{0, 0, 0}, {1, 1, 0.00001}]] 2.00004
Improve this answer
$\endgroup$
3
  • 1
    $\begingroup$ Look at my addendum. $\endgroup$ Commented Mar 4 at 20:49
  • $\begingroup$ Thanks for the research into the docs! A bit counterintuitive the use of SurfaceIntegral in 2D for scalar or vector fields $\endgroup$ Commented Mar 5 at 23:42
  • $\begingroup$ Even more counter intuitive is, that the region, over which the integral is taken,can be a n-1 D surface in a n D space. E.g. r = ImplicitRegion[x^2 + y^2 + z^2 == 1 && z >= 0, {x, y, z}]; Here we get the area of the half sphere, not the length of the circle. $\endgroup$ Commented Mar 6 at 9:21
3
$\begingroup$

Using ImplicitRegion can help, e.g.:

i = ImplicitRegion[a < x < 2 a && 0 < y < c, {x, y}]; A = A0 {y^2, -x^2}; si = SurfaceIntegrate[Curl[A, {x, y}], {x, y} \[Element] i, Assumptions -> {c > 0, a > 0}]; ln = Line /@ Partition[{{a, 0}, {2 a, 0}, {2 a, c}, {a, c}}, 2, 1, 1]; li = Total[LineIntegrate[A, {x, y} \[Element] #] & /@ ln] si == li

enter image description here

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.