6
$\begingroup$

I would like to plot a set of points in the same style as ListPlot3D does, but only in a non-convex region that I can specify (e.g. using a RegionFunction). Is there a simple solution for this?

Let me illustrate with an example.

Let's generate some sample points ...

Clear[regionFun] regionFun[{x_, y_}] := y < x^2 fun[{x_, y_}] := -Norm[{x, y} - {.5, .5}] pts = Select[Tuples[Range[0, 1, 0.01], 2], regionFun];

... and try to plot then in the region we're interested in:

ListPlot3D[ Append[#, fun[#]] & /@ pts, RegionFunction -> Function[{x, y}, regionFun[{x, y}]], InterpolationOrder -> 1 ]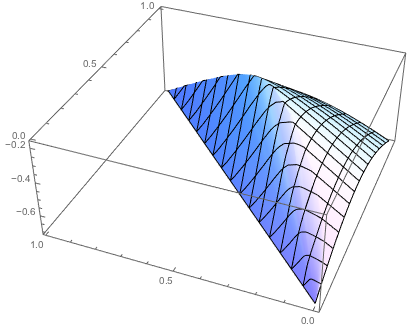

enter image description here

Notice that the plot occupies the complete convex hull of the points because of how the Delaunay triangulation was constructed for the interpolation.

What I would like to see instead is this:

Plot3D[fun[{x, y}], {x, 0, 1}, {y, 0, 1}, RegionFunction -> Function[{x, y}, regionFun[{x, y}]]]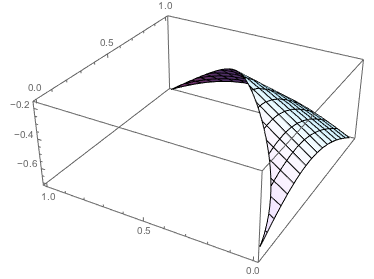

enter image description here

The only possible solution I see at the moment is to use an external tool to "manually" construct a Delaunay triangulation which is confined within a region and build the plot from that data. This, however, is a lot of work, so I thought I'd ask first if there's a simple solution.

Note that this is just a generated example dataset, not my real data. I can't use Plot3D for my real application, only ListPlot3D and related functions.

Improve this question
$\endgroup$
9
  • 2
    $\begingroup$ Interpolation + Plot3D works. $\endgroup$ Commented Nov 10, 2013 at 20:55
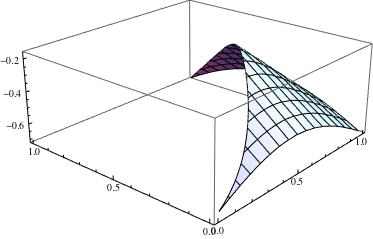
  • $\begingroup$ @rm-rf For a arbitrary point cloud on an unstructured grid we will have to accept the Interpolation::udeg message too! Interpolationorder will be constrained to one. $\endgroup$ Commented Nov 10, 2013 at 21:24
  • $\begingroup$ @PlatoManiac Right, but Szabolcs used order 1 anyway, so that shouldn't be a problem here. Szabolcs, I don't understand why you said you don't get nice plots... with ifun = Interpolation[Append[#, fun[#]] & /@ pts, InterpolationOrder -> 1, "ExtrapolationHandler" -> {(Indeterminate &), "WarningMessage" -> False}]; and MaxRecursion -> 6, I get a plot that's as good as the native Plot3D. $\endgroup$ Commented Nov 10, 2013 at 21:29
  • $\begingroup$ @PlatoManiac All built-in List* plotting functions that work on 2D data will only do linear interpolation for unstructured grids, so it's the same thing. $\endgroup$ Commented Nov 10, 2013 at 21:31
  • $\begingroup$ @rm-rf I also don't understand why I don't get nice plots for my real data, but I don't. This example I posted works perfectly. I guess my real data is nastier: dropbox.com/s/4xn79zcpnz81711/… Regardless, I'd accept your answer if you posted it as I'm using it now. (I did increase PlotPoints and MaxRecursion --- I think somehow the higher-than-order-1 adaptive sampler of Plot3D doesn't work well with the order-1 interpolation) $\endgroup$ Commented Nov 10, 2013 at 21:33

1 Answer 1

Reset to default
8
$\begingroup$

Using Interpolation with Plot3D and slightly increasing the MaxRecursion gives you a nice plot. Since you have an unstructured grid, the interpolation order will be restricted to 1.

ifun = Interpolation[Append[#, fun[#]] & /@ pts, InterpolationOrder -> 1, "ExtrapolationHandler" -> {(Indeterminate &), "WarningMessage" -> False}]; Plot3D[ifun[x, y], {x, 0, 1}, {y, 0, 1}, MaxRecursion -> 6, RegionFunction -> Function[{x, y}, regionFun[{x, y}]]]

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.