15
$\begingroup$

I'm doing this exercise in Wagner's book (p.78)

Mathematica graphics

, and this is my attempt:

Clear[curvature]; (*Define curvature function *) curvature[x_, y_, z_] := Module[{s, v, T}, s = {x, y, z}; v = D[s, t]; T = v/Norm[v]; Simplify[Norm[D[T, t]/Norm[v]]]] (* Apply function to Cos[t],Sin[t],t *) curvature[Cos[t], Sin[t], t]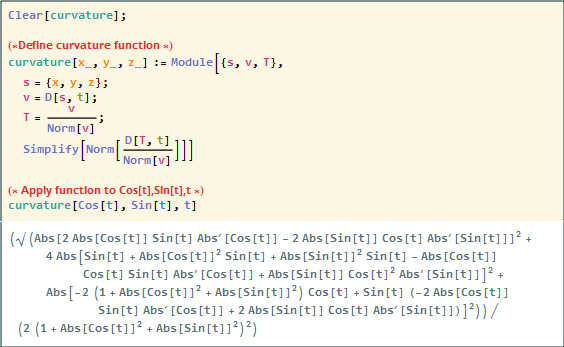

Mathematica graphics

As you could see I did not get the expected answer (1/2) when applying my curvature function.

It also would not reduce even when a value for t was substituted:

curvature[Cos[t], Sin[t], t] /. t -> 4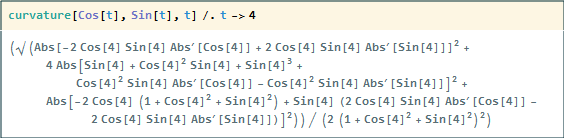

Mathematica graphics

However, following Wagner's solution where he defines a separate magnitude function does work:

Clear[curvature]; (* Define function to find magnitude of a vector *) mag[vec_] := Sqrt[vec.vec] (* Define curvature function *) curvature[x_, y_, z_] := Module[{s, v, T}, s = {x, y, z}; v = D[s, t]; T = v/mag[v]; Simplify[mag[D[T, t]/mag[v]]]] (* Apply function to Cos[t],Sin[t],t *) curvature[Cos[t], Sin[t], t]

Mathematica graphics

It seems pretty clear that using Norm to find the magnitude of a vector does not work in this case. More specifically, using Norm doesn't seem to simplify trigonometric results unless the t is substituted

Norm[{Cos[t], Sin[t]}] Norm[{Cos[t], Sin[t]}] /. t -> 4 // Simplify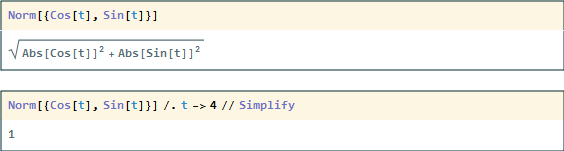

Mathematica graphics

I'm very fuzzy on my matrix knowledge so I'd really appreciate an explanation on why Norm doesn't seem to return the expected answer in this case. Also, is there any other way to find a vector's magnitude that will give the correct answer without defining a new function?

Improve this question
$\endgroup$
2

3 Answers 3

Reset to default
15
$\begingroup$

Norm in general assumes complex arguments and uses Abs to provide for that:

Norm[{x, y}]

Sqrt[Abs[x]^2 + Abs[y]^2]

For real elements, you can either add an assumption for Simplify or manually get rid of Abs beforehand:

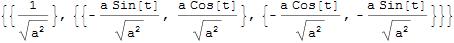
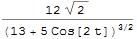
Simplify[Norm[{Cos[t], Sin[t]}], Element[t, Reals]] Simplify[Norm[{Cos[t], Sin[t]}] /. Abs -> Identity]

1

1

This now returns the desired result for real t:

curvature[x_, y_, z_] := Module[{s, v, T}, s = {x, y, z}; v = D[s, t]; T = v/Norm[v]; Simplify[Norm[D[T, t]/Norm[v]] /. Abs -> Identity]] curvature[Cos[t], Sin[t], t]

1/2

Improve this answer
$\endgroup$
7
$\begingroup$

EDIT

With V10 we can use

ArcCurvature[2 {Cos[t], Sin[t]}, t]

1/2

Or

FrenetSerretSystem[a {Cos[t], Sin[t]}, t]

enter image description here

yielding curvature, tangent, and normal

Original answer

An alternative:

$Assumptions = t \[Element] Reals; J[{x_, y_}] := {-y, x} Curvature[a_][t_] := a''[t].J[a'[t]]/Norm[J[a'[t]]]^3 // Simplify circle[a_][t_] := {a Cos[t], a Sin[t]} Curvature[circle[2]][t]

enter image description here

ellipse[a_, b_][t_] := {a Cos[t], b Sin[t]} Curvature[ellipse[2, 3]][t]

enter image description here

Curvature[ellipse[2, 3]][Pi]

enter image description here

$Assumptions = True; (* Clear *)
Improve this answer
$\endgroup$
2
  • $\begingroup$ Thank you for your answer. Could you help me understand why you defined a function with 2 parameters in separate brackets? $\endgroup$ Commented Jul 3, 2014 at 19:45
  • $\begingroup$ @seismatica I think it's just a matter of personal taste. Makes code clearer for me in the ellipse-case (t vs. Pi). $\endgroup$ Commented Jul 3, 2014 at 19:58
6
$\begingroup$

Here is a version of curvature that uses Mathematica machinery not available to Wagner, who used V3. 

curvature[x_, y_, z_] := Module[{s, v, vMag, T}, Block[{$Assumptions = {{x, y, z} ∈ Reals}}, s = {x, y, z}; v = D[s, t]; vMag = Surd[v.v, 2]; T = v/vMag; Simplify[Norm[D[T, t]/vMag]]]] curvature[Cos[t], Sin[t], t] 
1/2
Improve this answer
$\endgroup$
3
  • 1
    $\begingroup$ That post would have been also great from @Sjoerd: Surd by Sjoerd :D $\endgroup$ Commented Jul 3, 2014 at 11:24
  • 3
    $\begingroup$ @YvesKlett. Perhaps Sjoerd thought that using Surd to eliminate Abs was absurd :D $\endgroup$ Commented Jul 3, 2014 at 11:28
  • $\begingroup$ hehe, I had that one coming :-) $\endgroup$ Commented Jul 3, 2014 at 11:29

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.