Consider this example:
ds = Dataset @ Transpose[<|"a" -> {1, 2, 3, 4, 3, 2, 1}, "b" -> {6, 5, 4, 3, 2, 1, 0}|>, AllowedHeads -> All] 
Now say I need to work with the ratios of these two values. This works fine:
ds[;;-2, #a/#b &] 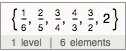
But this fails:
ds[All, #a/#b &] 
It would be easier for me to just get a result with some ComplexInfinities. Does the operation fail by desgin or oversight? Is there a workaround? Should I just use
ds[All, Quiet[#a/#b] &] all the time or is there a more general solution? Off[General::infy] doesn't prevent this from failing, though the failure message can't be displayed properly.

FailureAction. $\endgroup$