6
$\begingroup$

Consider the MathieuCharacteristicA function, which is a piecewise function according to the documentation. The discontinuity happens at integer number.

With[{V0 = -1}, Plot[MathieuCharacteristicA[κ, V0], {κ, -2.5, 2.5}]]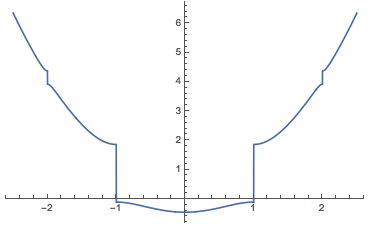

enter image description here

Consider the point approaching k=2 from the left side , and plot the Mathieu funtions near that point. 

ParallelTable[ Plot[Evaluate@ With[{V0 = -1, κ = 2 - ϵ}, Re@MathieuC[MathieuCharacteristicA[κ, V0], V0, z]], {z, -10, 10}, PlotRange -> All, ImageSize -> Medium], {ϵ, {10^-8, 15/10*10^-8, 18/10*10^-8, 2*10^-8}}]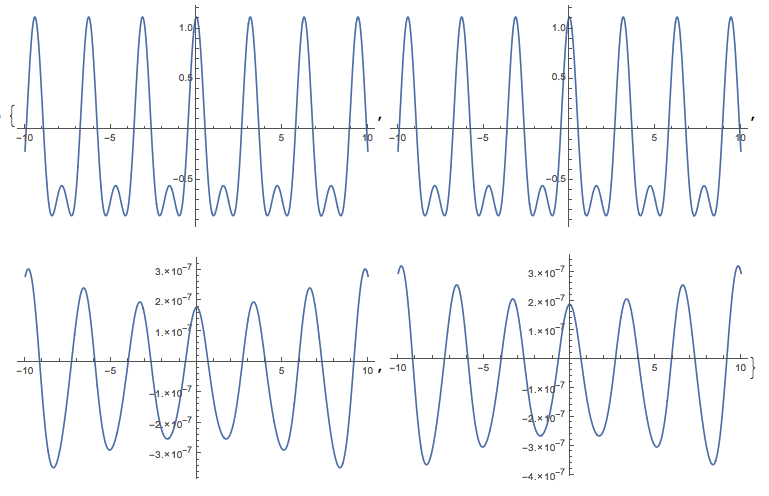

enter image description here

We see that from points k=2-10^-8 , k=2-1.5*10^-8 to points k=1.8*^-8, k=2*^-8, there are big discontinouity. Why does this big discontinuity happen in the Mathieu function, even we are still away from the piecewise point? Which result is correct?

Moreover, as I increase the working precision, the results changes. Which results should I trust?

ParallelTable[ Plot[Evaluate@ With[{V0 = -1, κ = 2 - ϵ}, Re@MathieuC[MathieuCharacteristicA[κ, V0], V0, z]], {z, -10, 10}, PlotRange -> All, ImageSize -> Medium, WorkingPrecision -> 50], {ϵ, {10^-8, 15/10*10^-8, 18/10*10^-8, 2*10^-8}}]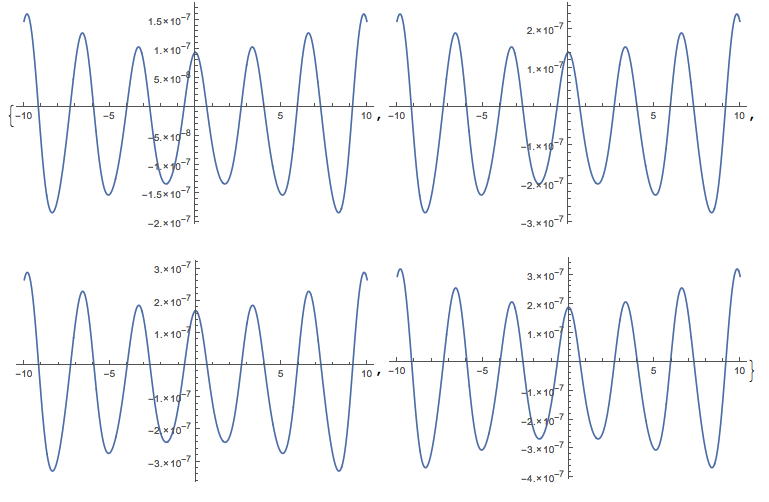

enter image description here

Update:

More strange behavior

NLimit[ Re@MathieuC[MathieuCharacteristicA[κ, -1], -1, 0], κ -> 2, Direction -> 1, WorkingPrecision -> 100] (* 0.000026560352729499428275267693547091828644960849846890155742135607985075453865741662994877041 *) N[ Table[Re@MathieuC[MathieuCharacteristicA[2 - ϵ, -1], -1, 0], {ϵ, {10^-6, 10^-8, 10^-10, 10^-20, 10^-40, 10^-60, 10^-100}}], 100] (* \ {9.375519741470728355592491183508603286638427801561870220416306315833951776806837902179623867179198570*10^-6, 9.375519742493871990285719573456924995106820123921565403331967009687923231481580841077469030562191305*10^-8, 9.375519742493974304649207591451232553957148872416907065490732452953108780592926489536671069329119067*10^-10, 9.375519742493974314881667185336397875216528878100913700967589255793432748631135267810942389900367393*10^-20, 9.375519654864253585910474819580416042344587293945440367769556457939085038181962308922619162634748808*10^-40, 1.114388591781733115021002428520876171768008184684161143978162399223107768160400228809114697590700165, 1.114388591781733115021002428520876171768008184684161143978162399223107768160400228809114697590700165} *)

What's the correct limit for k->2 ?

Improve this question
$\endgroup$
2
  • 1
    $\begingroup$ Mathematica doesn't like Mathieu functions $\endgroup$ Commented Aug 27, 2014 at 18:30
  • 1
    $\begingroup$ Definitely trust the one done with WorkingPrecision other than the default, which is MachinePrecision. In other words, precision tracking is off by default for Plot. This is a very bad thing for numerically sensitive functions such as the Mathieu functions. $\endgroup$ Commented May 16, 2015 at 17:20

1 Answer 1

Reset to default
5
$\begingroup$

If we compare N on the exact values with the MachinePrecision values, we see that the second two graphs (of the first quartet) look correct and the first two are wrong.

Block[{z = 0}, Table[With[{V0 = -1, κ = 2 - ϵ}, Re@MathieuC[MathieuCharacteristicA[κ, V0], V0, z]], {ϵ, {15/10*10^-8, 18/10*10^-8}}] ] N[%, 6] (* {MathieuC[MathieuCharacteristicA[399999997/200000000, -1], -1, 0], MathieuC[MathieuCharacteristicA[999999991/500000000, -1], -1, 0]} {1.4063279613740616126811177594156`6.*^-7, 1.6875935536488557009743434482017`6.*^-7} *) Block[{z = 0.}, Table[With[{V0 = -1, κ = 2 - ϵ}, Re@MathieuC[MathieuCharacteristicA[κ, V0], V0, z]], {ϵ, {15/10*10^-8, 18/10*10^-8}}] ] (* {1.11439, 1.7027*10^-7} *)

As the OP showed, this can be seen in the plots, if the WorkingPrecision is set high enough. Clearly, one should trust the second quartet of plots if one is going to trust Mathematica at all. N[expr, n] will report the answer with a precision that is supposed to be correct.

Edit

As @acl has observed Mathieu functions are difficult functions numerically. I would expect it to be even more difficult near a singular point of MathieuCharacteristicA[κ, -1], where a little round-off error causes a discontinuous jump.

The following seem entirely consistent with the left-hand limit being zero, which is at the same time not inconsistent with the OP's evaluation of NLimit.

N@Block[{$MaxExtraPrecision = 500}, NLimit[Re@MathieuC[MathieuCharacteristicA[κ, -1], -1, 0], κ -> 2, Direction -> 1, WorkingPrecision -> 300, Terms -> 50] ] N[Re@MathieuC[MathieuCharacteristicA[2, -1], -1, 0], 10] N@Block[{$MaxExtraPrecision = 500}, NLimit[Re@MathieuC[MathieuCharacteristicA[κ, -1], -1, 0], κ -> 2, Direction -> -1, WorkingPrecision -> 300, Terms -> 50] ] (* -1.49047*10^-45 0.8157268391 1.15361 *)

The inconsistencies observed by the OP seem to be due to round-off error. I suppose one complaint is that Mathematica issues no warnings in evaluating the OP's examples, especially the ones involving N applied to an exact value.

Improve this answer
$\endgroup$
11
  • $\begingroup$ Why does this big discontinuity happen in the Mathieu function, even we are still away from the piecewise point? You think Mathematica just got wrong? $\endgroup$ Commented Aug 27, 2014 at 17:52
  • $\begingroup$ @xslittlegrass Round-off error, no? (Perhaps I should point it out explicitly?) $\endgroup$ Commented Aug 27, 2014 at 17:56
  • $\begingroup$ I'm not convinced it's simply the round-off error, see my updates. $\endgroup$ Commented Aug 27, 2014 at 19:57
  • 1
    $\begingroup$ @xslittlegrass Try Block[{$MaxExtraPrecision = 500}, N[Table[Re@MathieuC[MathieuCharacteristicA[2 - \[Epsilon], -1], -1, 0], {\[Epsilon], {10^-6, 10^-8, 10^-10, 10^-20, 10^-40, 10^-60, 10^-100}}], 300]] (I wouldn't think 100 digits was enough for 2 - 10^-100, which requires 101 digits just for itself.) $\endgroup$ Commented Aug 27, 2014 at 20:03
  • 1
    $\begingroup$ @xslittlegrass What calculations does NLimit actually do? $\endgroup$ Commented Aug 27, 2014 at 20:28

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.