2
$\begingroup$

I have a grid of values generated from a MATLAB evaluation. Most of these elements are 0, some 0.5 and the remainder 1. I'd like to write a mathematica script which reads in the CSV and then, in every position where there is a 1, I'd like it to create a Graphics3D red sphere of radius 1, and in every position where there is an 0.5, a green sphere of radius 1. However, I'm not sure whether the best approach is to use loops or something more natural in Mathematica. To illustrate, here's a sample 5 x 5 matrix; 

M = {{0, 0, 0, 0, 0.5}, {1, 0, 0, 0, .5}, {0, 0, 0, 0, 0.5}, {1, 0, 1, 0, 0}, {0, 0, 0, 0, 1}};

I can get all the ones and halfs from the grid as follows;

Ones = Position[M, 1]; Halfs = Position[M, 0.5]; OneLength = Length[Ones]; HalfLength = Length[Halfs]; Xpos = Part[Part[Ones, 1], 1]; Ypos = Part[Part[Ones, 1], 2];

Where I get the lengths in case I need to run a loop - which I'm trying to avoid. Similarly the Xpos and Ypos give a co-ordinate I could loop but I'm sure there's an easier way. In essence, I want to end up with a picture like this for the sample data above;

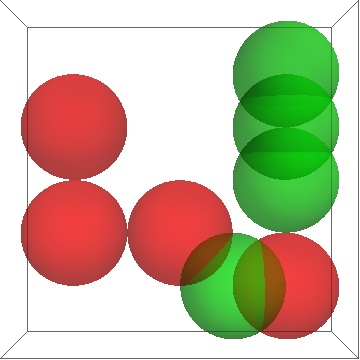
enter image description here

In the example above, I generated it manually using 

j1 = Graphics3D[{Opacity[0.5], Green, Sphere[{5, 6 - 1, 0}]}]; j2 = Graphics3D[{Opacity[0.5], Green, Sphere[{5, 6 - 2, 0}]}]; j3 = Graphics3D[{Opacity[0.5], Green, Sphere[{5, 6 - 3, 0}]}]; j4 = Graphics3D[{Opacity[0.5], Green, Sphere[{4, 6 - 5, 0}]}]; g1 = Graphics3D[{Opacity[0.5], Red, Sphere[{1, 6 - 2, 0}]}]; g2 = Graphics3D[{Opacity[0.5], Red, Sphere[{1, 6 - 4, 0}]}]; g3 = Graphics3D[{Opacity[0.5], Red, Sphere[{3, 6 - 4, 0}]}]; g4 = Graphics3D[{Opacity[0.5], Red, Sphere[{5, 6 - 5, 0}]}]; Show[j1, j2, j3, j4, g1, g2, g3, g4]

Notice that I've subtracted the y element from 6, as Matlab starts its y-count from the top down rather than from the axis, so any matrix I get in from Matlab will need something like this to Y-flip. Is there a clever way to automate this, using table or otherwise which will circumvent loops? If loops are required, what is the most efficient way of creating one? I will eventually be working with 200 x 200 arrays so manual manipulation would be best avoided! Thanks in advance...

Improve this question
$\endgroup$
1
  • $\begingroup$ Your manual version has eight spheres, while the matrix only has seven non-null entries. ;) $\endgroup$ Commented Mar 11, 2015 at 12:26

2 Answers 2

Reset to default
3
$\begingroup$

Using Map, you can avoid looping:

Graphics3D[{Opacity[0.5], {Red, Sphere /@ (Position[M, 1] /. {x_, y_} :> {x, 6 - y, 0})}, {Green, Sphere /@ (Position[M, .5] /. {x_, y_} :> {x, 6 - y, 0})}}]

or a little shorter (but more nerdy):

Graphics3D[{Opacity[0.5], {#1,Sphere/@#2}&@@{#[[2]],Position[M,#[[1]]]/.{x_,y_}:>{x,6-y,0}}&/@{{1,Red},{0.5,Green}}}]

With some more options, you get your desired 3D-view:

Graphics3D[{Opacity[0.5], {#1,Sphere/@#2}&@@{#[[2]],Position[M,#[[1]]]/.{x_,y_}:>{x,6-y,0}}&/@{{1,Red},{0.5,Green}}}, ViewPoint->Above,ViewVertical->{0,0,1},Boxed->False,AxesOrigin->{0,0,0}, Axes->{True,True,False},AxesLabel->{"x","y","z"}]

3D-view

Improve this answer
$\endgroup$
2
  • $\begingroup$ Brilliant - cheers! $\endgroup$ Commented Mar 11, 2015 at 18:42
  • $\begingroup$ @DRG: Glad to hear to have been of some help! $\endgroup$ Commented Mar 11, 2015 at 20:40
6
$\begingroup$

The MapIndexed function works very nicely for this, as it provides both the value of the array element, and a list representing its position. I wasn't golfing here, so I used pattern matching on function arguments for the rest:

draw[0, _] = {}; draw[v : Except[0], {x_, y_}] := {v /. {0.5 -> Green, 1 -> Red}, Sphere[{x, 6 - y, 0}]}; Graphics3D[{ Opacity[0.5], MapIndexed[draw, M, {2}]}]
Improve this answer
$\endgroup$
2
  • $\begingroup$ +1. MapIndexed seems the most appropriate tool. I might use Condition with numeric tests, esp. since the data is coming from outside Mathematica. E.g. draw[zero_, _] /; zero == 0 :=... and v /. {v0_ /; v == 0.5 -> Green, v0_ /; v == 1 -> Red}. (For instance 1 matches only the Integer and not the Real number 1, and the numbers might be off by machine epsilon or so. Using Equal allows for such differences.) $\endgroup$ Commented Mar 11, 2015 at 13:29
  • $\begingroup$ Great answer, will use this technique for something else I have in mind! Thanks $\endgroup$ Commented Mar 11, 2015 at 18:42

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.