9
$\begingroup$

I would like to produce a graphic like this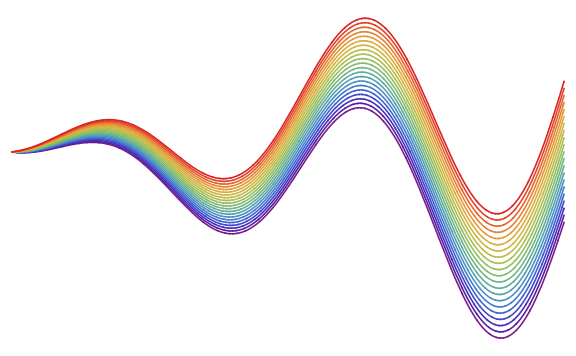rainbow

but with a continous color gradient between the outer curves.

Is it possible to achieve this by using the Filling option?

Code for the sake of completeness:

Plot[ Evaluate@Table[(Sin[x]+o)*x,{o,-0.5,0.5,0.05}],{x,0,4*Pi}, PlotStyle->Table[ColorData["Rainbow", i/20], {i,0,20}], ImageSize->Large, Axes->False ]
Improve this question
$\endgroup$
9
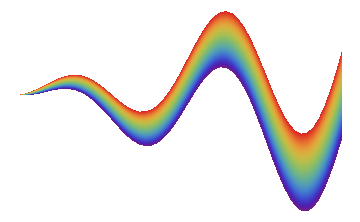
  • $\begingroup$ Yes, actually there is an example in the Filling documentation under the Scope -> Filing Style. I would start there. $\endgroup$ Commented Jul 19, 2015 at 20:52
  • $\begingroup$ @Szabolcs I don't think filling supports gradients in the y direction. For 20 curves as in OP appropriate filling between the curves would give roughly the correct result, but it wouldn't be a truly smooth gradient. $\endgroup$ Commented Jul 19, 2015 at 21:20
  • 1
    $\begingroup$ @LLlAMnYP It does support vertical gradients. The example I cited has one. Here's an example: Plot[{x (Sin[x] - .5), x (Sin[x] + .5)}, {x, 0, 4 Pi}, Filling -> {1 -> {2}}, ColorFunction -> Function[{x, y}, GrayLevel[(y - x (Sin[x] - .5))/x]], ColorFunctionScaling -> False]. But you're right, it won't work for a rainbow colour scheme, even though it does for grayscale. The reason is that it will only use linear interpolation between the two RGB colours on the upper an lower points. This interpolation (done by VertexColors) doesn't care about colour schemes, can't have all rainbow colours. $\endgroup$ Commented Jul 19, 2015 at 21:26
  • $\begingroup$ @LLlAMnYP The ParametricPlot creates many small polygons in the middle, each of which will interpolates linearly between different sets of colours. So now we can have a full rainbow spectrum. It's also simpler than Filling. +1! $\endgroup$ Commented Jul 19, 2015 at 21:27
  • $\begingroup$ @Szabolcs my documentation for Filling does not have any similar examples. Is this a new feature in 10.2? $\endgroup$ Commented Jul 19, 2015 at 21:29

1 Answer 1

Reset to default
15
$\begingroup$

Such a filling is possible with ParametricPlot.

ParametricPlot[{x, x (Sin[x] + o)}, {x, 0, 4 Pi}, {o, -0.5, .5}, ColorFunction -> (ColorData["Rainbow"][#4] &), AspectRatio -> 1/GoldenRatio, Frame -> False, Axes -> False, BoundaryStyle -> None]

result

Improve this answer
$\endgroup$
1
  • $\begingroup$ updated to match styling in the OP $\endgroup$ Commented Jul 19, 2015 at 21:17

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.