7
$\begingroup$

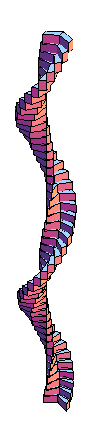
I define following functions:

helix[a_, b_][t_] := {a*Cos[t], a*Sin[t], b*t} listept = Table[helix[0.35, 0.35][t], {t, 0, 4 Pi, .25}]; bezierint = Graphics3D[Cuboid[{#, # + 0.1}] & /@ listept] tube = Graphics3D[{Opacity[0.25], RGBColor[1, 3, 0], Cylinder[{{0, 0, 0}, {0, 0, 1.55 Pi}}, 0.75]}] Show[{bezierint, tube}]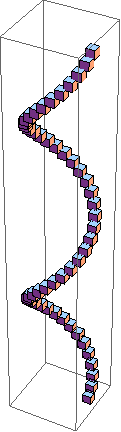

Mathematica graphics

and now I would like to substitute each ordinary Cuboid defined in bezierint with fancy Cuboid defined as follow:

box1 = GeometricTransformation[Cuboid[{0, 0, 0}], ShearingMatrix[Pi/4, {1,0, 0}, {-1, 1, 0}]] box2 = GeometricTransformation[Cuboid[{1, 1, 0}], ShearingMatrix[-Pi/4, {1, 0, 0}, {-1, 1, 0}]] Graphics3D@{box1, box2}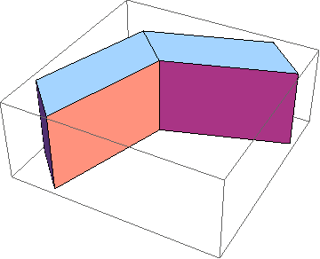

Mathematica graphics

simulateneously mentaining the repeatability of the pattern.

I have used many approaches but up to now all were unsuccesful. Did anyone had to deal before with such task?

Improve this question
$\endgroup$
1
  • $\begingroup$ Welcome to Mathematica.SE! I suggest the following: 1) Browse common pitfalls. 2) As you receive help, try to give it too, by answering questions in your area of expertise. 3) Take the tour and check the help center! 4) When you see good questions and answers, vote them up using the triangles. Also, please remember to accept an answer if it solves your problem, by clicking the checkmark! $\endgroup$ Commented Sep 23, 2015 at 6:15

1 Answer 1

Reset to default
12
$\begingroup$

Perhaps:

gt = GeometricTransformation; box = gt[{box1, box2}, ScalingTransform[.1 {1, 1, 1}]]; cc[{x_, y_, z_}] := gt[gt[box, RotationTransform[{{1, 1, 0}, {x, y, 0}}]], TranslationTransform[{0, 0, z}]] Graphics3D[cc /@ listept]

Mathematica graphics

Edit

A small generalization, just for fun:

gt = GeometricTransformation; box = gt[{box1, box2}, ScalingTransform[.1 {1, 1, 1}]]; cg[{x_, y_, z_}, pat_] := gt[gt[box, RotationTransform[{{1, 1, 0}, pat[x, y, z]}]], TranslationTransform[{0, 0, z}]] gf[pat_] := Graphics3D[cg[#, pat] & /@ listept] gf /@ {Function[{a, b, c}, {a, b, 0}], Function[{a, b, c}, {a, b, Sin@c}], Function[{a, b, c}, {a, -b, c^2}], Function[{a, b, c}, {a^2, b, 0}]}

Mathematica graphics

Improve this answer
$\endgroup$

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.