Find the explicit solution of the integral

Question

I want to calculate the integral:

$$A_n=\int_0^{2\pi}\cos^{2n}(\theta-\theta_0)\mathrm d\theta$$

assuming that we are familiar with the relation:

$$\cos^{2n}x=\frac1{2^{2n}}\binom{2n}{n}+\frac1{2^{2n-1}}\sum_{k=0}^{n-1}\binom{2n}{k}\cos2(n-k)x$$ The answer should be:
$$A_n=\frac{\pi}{2^{2n-1}}\binom{2n}{n}$$

The code that I've used is the following:

$Assumptions = n ∈ Integers; substitute = {(Cos[x_])^(2 n) -> 1/2^(2 n) Binomial[2 n, n] + 1/2^(2 n - 1) * Sum[Binomial[2 n, k] Cos[2 (n - k) x], {k, 0, n - 1}]};

But I see that substitution is not done correctly:

Cos[θ - μ]^(2 n) /. substitute

$2^{-2 n} \binom{2 n}{n}+2^{-2 n} e^{-2 i n (\theta -\mu )} \left(-\binom{2 n}{n} e^{2 i n (\theta -\mu )} \, _2F_1\left(1,-n;n+1;-e^{-2 i (\theta -\mu )}\right)-\binom{2 n}{n} e^{2 i n (\theta -\mu )} \, _2F_1\left(1,-n;n+1;-e^{2 i (\theta -\mu )}\right)+e^{4 i n (\theta -\mu )} \left(1+e^{-2 i (\theta -\mu )}\right)^{2 n}+\left(1+e^{2 i (\theta -\mu )}\right)^{2 n}\right)$
And the integral is calculated as:

A = Integrate[Cos[θ - μ]^(2 n) /. substitute, {θ, 0, 2 Pi}, Assumptions -> 0 <= μ <= 2 Pi]

$\text{Integrate}\left[2^{-2 n} \binom{2 n}{n}+2^{-2 n} e^{-2 i n (\theta -\mu )} \left(-\binom{2 n}{n} e^{2 i n (\theta -\mu )} \, _2F_1\left(1,-n;n+1;-e^{-2 i (\theta -\mu )}\right)-\binom{2 n}{n} e^{2 i n (\theta -\mu )} \, _2F_1\left(1,-n;n+1;-e^{2 i (\theta -\mu )}\right)+e^{4 i n (\theta -\mu )} \left(1+e^{-2 i (\theta -\mu )}\right)^{2 n}+\left(1+e^{2 i (\theta -\mu )}\right)^{2 n}\right),\{\theta ,0,2 \pi \},\text{Assumptions}\to 0\leq \mu \leq 2 \pi \right]$
Is there any way to force mathematica calculate the explicit solution of the integral?

Edit: I wonder why I get the result:

Integrate[(Cos[t - t0])^(2 n), {t, 0, 2 Pi}, Assumptions -> n ∈ Integers && t0 ∈ Reals && 0 <= t0 < 2 Pi] // AbsoluteTiming (* {133.223, Integrate[Cos[t - t0]^(2 n), {t, 0, 2 \[Pi]}, Assumptions -> n ∈ Integers && t0 ∈ Reals && 0 <= t0 < 2 \[Pi]]} *)

After considering all the information I gained from following links:
Singular integral mathematica
Correct way to integrate a certain function
Bug in mathematica analytic integration?
Suspected bug in Integrate

I also wrote the following code:

r := RandomReal[{0, 2 Pi}] Integrate[(Cos[t - t0])^(2 n) /. t0 -> r, {t, 0, 2 Pi}, Assumptions -> n ∈ Integers] // AbsoluteTiming (* {6.18195, 1/((0.5 + 1. n) Gamma[ 1. + n]) ((1.77245 + 1.77245 E^((0. + 6.28319 I) n)) Gamma[ 1.5 + n] + Gamma[1. + n] (-0.421391 E^(-0.342092 n) Hypergeometric2F1[0.5, 0.5 + 1. n, 1.5 + 1. n, 0.710283] + 0.421391 E^(-0.342092 n) Hypergeometric2F1[0.5, 0.5 + 1. n, 1.5 + 1. n, 0.710283]))} *)

seems that I can never reach the solution

(* {19.1049, ConditionalExpression[((1 + (-1)^(2 n)) Sqrt[π] Gamma[1/2 + n])/Gamma[1 + n], Cos[x0] >= 0 && 2 π < x0 <= (5 π)/2]} *)

expressed by @MichaelE2

Edit: I finally wrote the following code and I get the result except that I don't understand why is Global needed in my answer:

int = Simplify[(Cos[t - t0])^(2 n) Dt[t] /. t -> t0 + x // TrigExpand] /. {Dt[t0] -> 0, Dt[x] -> 1} (* Cos[x]^(2 n) *) Integrate[int, {x, -t0, 2 Pi - t0}, Assumptions -> n ∈ Integers && n > 0 && t0 ∈ Reals && 0 <= t0 < 2 Pi] (* ConditionalExpression[((1 + (-1)^(2 Global`n)) Sqrt[\[Pi]] Gamma[1/2 + Global`n])/Gamma[1 + Global`n], Global`t0 > 0 && 2 Global`t0 <= \[Pi]] *)

Here we are again. The antiderivative is easily determined by Mathematica but it is not continuous in the interval of integration but there are jumps which have to be taken into account when using the fundamental theorem of calculus. See e.g. my answer to mathematica.stackexchange.com/questions/92044/… — Dr. Wolfgang Hintze
– Dr. Wolfgang Hintze, Commented Oct 13, 2015 at 16:22
@Dr.WolfgangHintze which is true? 1- fundamental theorem of calculus says that the integrand $f(x)$ in $\int_a^b f(x)dx=F(x)$ should be continuous on the $[a,b]$ interval. 2- fundamental theorem of calculus says that the antiderivative $F(x)$ in $\int_a^b f(x)dx=F(x)$ should be continuous on the $[a,b]$ interval. Consider links : 1- Mathematica and the Fundamental Theorem of Calculus 2- Fundamental Theorems of Calculus — Sepideh Abadpour
– Sepideh Abadpour, Commented Oct 14, 2015 at 19:47
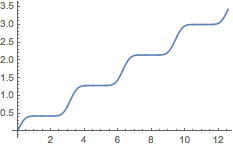
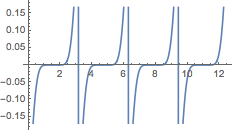
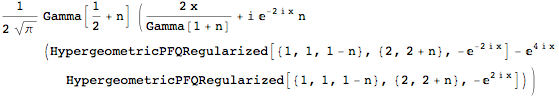
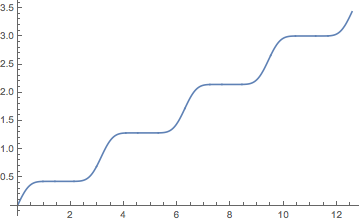
@sepideh I'm afraid the only suggestion might be to restart your kernel and try the integral fresh. It's rare that M returns different results on different systems (probably never in the case of Integrate). User variables normally are created in the Global` context, but I don't know why it shows up explicitly printed in the output. — Michael E2
– Michael E2, Commented Oct 15, 2015 at 11:56

Community · Accepted Answer · 2017-04-13 12:55:57Z

I've seen something like this before, something like Correct way to integrate a certain function or Suspected bug in Integrate perhaps, in which Cos[x - x0] and Cos[x] lead to different results in Integrate. It's worth knowing this happens and doing the translation by hand can help.

Assuming[n ∈ Integers && n > 0 && x0 ∈ Reals, Integrate[Cos[x - x0]^(2 n), {x, 0, 2 Pi}] ] // AbsoluteTiming (* {19.1049, ConditionalExpression[((1 + (-1)^(2 n)) Sqrt[π] Gamma[1/2 + n])/Gamma[1 + n], Cos[x0] >= 0 && 2 π < x0 <= (5 π)/2]} *)

After translation:

Assuming[n ∈ Integers && n > 0, Integrate[Cos[x]^(2 n), {x, 0, 2 Pi}] ] // AbsoluteTiming (* {1.34932, (2^(1 + 2 n) π^2)/(Gamma[1/2 - n]^2 Gamma[1 + 2 n])} *)

These are equivalent to Pi/2^(2 n - 1) Binomial[2 n, n].

Addendum

For what it's worth, here's a way to get a general antiderivative valid for over all real intervals. First note that Mathematica can find such an antiderivative for an explicit numeric integer n but not for a symbolic one.

Block[{n = 4}, With[{i = Integrate[Cos[x]^(2 n), x]}, Plot[i, {x, 0, 4 Pi}] ]] With[{i = Integrate[Cos[x]^(2 n), x, Assumptions -> n > 0 && n ∈ Integers]}, Block[{n = 4}, Plot[i, {x, 0, 4 Pi}] ]]

Mathematica graphics

Let's see if we can find a pattern in the antiderivatives. First find a bunch:

seq = Table[Integrate[Cos[x]^(2 n), x], {n, 30}];

The all have a linear part and a sum of sines.

seq[[4]] (* (35 x)/128 + 7/32 Sin[2 x] + 7/128 Sin[4 x] + 1/96 Sin[6 x] + Sin[8 x]/1024 *)

FindSequenceFunction can find the patterns in the coefficients. First the linear coefficient.

xcoeff = FindSequenceFunction[Coefficient[seq, x]];

Then the coefficients for the sines, which depend on n and the coefficient 2 k inside the sines.

seq2 = Table[FindSequenceFunction[Coefficient[seq, Sin[2 k x]]], {k, 12}];

These, too, have a pattern. Here is a typical one, with two Pochhammer symbols, an expanded Pochhammer symbol, and a numeric coefficient.

Through[seq2[n]][[4]] (* ((-3 + n) (-2 + n) (-1 + n) n Pochhammer[9/2, -4 + n])/(24576 Pochhammer[9, -4 + n]) *)

We'll get each piece separately, the Pochhammer in the numerator, the one in the denominator, and everything else:

First@Cases[#, _Pochhammer] & /@ Through[seq2[n]]; npoch = FindSequenceFunction /@ Transpose[% /. Pochhammer -> List]; npoch = Thread[npoch, Function] /. List -> Pochhammer; First@Cases[#, Power[p_Pochhammer, -1] :> p] & /@ Through[seq2[n]]; dpoch = FindSequenceFunction /@ Transpose[% /. Pochhammer -> List]; dpoch = Thread[dpoch, Function] /. List -> Pochhammer; nonpoch = FindSequenceFunction[Through[seq2[n]] /. HoldPattern@Pochhammer[__] -> 1];

What the final coefficient looks like:

nonpoch[k] npoch[k]/dpoch[k] (* ((-1)^(1 + k) 4^-k n Pochhammer[1/2 (1 + 2 k), -k + n] * Pochhammer[1 - n, -1 + k])/(k Pochhammer[2, -1 + k] Pochhammer[1 + 2 k, -k + n]) *)

Now, Sum can actually sum all these things!

i = Block[{n}, xcoeff[n] x + Sum[nonpoch[k] npoch[k]/dpoch[k]*Sin[2 k x], {k, n}] // FullSimplify ]

Mathematica graphics

The plot for n = 4:

Block[{n = 4}, Plot[i, {x, 0, 4 Pi}] ]

Mathematica graphics

Now, I wonder if Mathematica will ever be able to do that? (Probably.)

Back to the OP's question, here's the definite integral, which again agrees with the OP's sought-after answer:

First@Differences[i /. {{x -> 0}, {x -> 2 Pi}}] % - Pi/2^(2 n - 1) Binomial[2 n, n] // FullSimplify (* (2 Sqrt[π] Gamma[1/2 + n])/Gamma[1 + n] 0 *)

@sepideh In this case, it appears the bug has been fixed (both answers are correct). It's not too surprising (to me) it takes longer or looks different, imo. The x - x0 probably invokes a lot of checking due to the symbolic parameter x0. — Michael E2
– Michael E2, Commented Oct 14, 2015 at 10:23
Which version of mathematica are you using? I just entered your code in version 10.2 but the answer is different [Assuming[n \[Element] Integers && n > 0 && x0 \[Element] Reals, Integrate[Cos[x - x0]^(2 n), {x, 0, 2 Pi}]] // AbsoluteTiming (*{132.872, \!$ \*SubsuperscriptBox[\(\[Integral]$, $0$, $2\ \[Pi]$]$ \*SuperscriptBox[\(Cos[x - x0]$, $2\ n$] \[DifferentialD]x\)\)}*)] — Sepideh Abadpour
– Sepideh Abadpour, Commented Oct 14, 2015 at 20:45
@sepideh I'm using V10.2 Mac OSX. The new result you get in the OP seems numerically equivalent to my answer. Note that there are some issues with precision in the numerics, and the result is better if the precision is higher (e.g. r := RandomReal[{0, 2 Pi}, WorkingPrecision -> 20]). In general, using approximate coefficients in Integrate, generally used for exact solutions, sometimes produces unreliable results because of numerics issues. That does not seem to be the case here, though. Just tried mine again: Got the same result, although it took 120s the 1st time, 20s the 2nd+ times. — Michael E2
– Michael E2, Commented Oct 15, 2015 at 2:32

Dr. Wolfgang Hintze · Accepted Answer · 2015-10-15 17:56:12Z

Having been very brief (and impolite, sorry for that) in my comment, due to lack of time, I'd like to show now how to proceed. The method is not automatic, but it is "man-machine-cooperation" which will lead to the result. It might be interesting despite the complete solution with Mathematica given by Michael E2, because it applies to more general situations.

First step: antidervative

The antiderivative of the integrand is given by

fA[n_, t_, t0_] = Integrate[Cos[t - t0]^(2 n), t] (* Out[1]= -(( Cos[t - t0]^(1 + 2 n) Csc[t - t0] Hypergeometric2F1[1/2, 1/2 + n, 3/2 + n, Cos[t - t0]^2] Sqrt[Sin[t - t0]^2])/(1 + 2 n)) *)

Second step: check of continuity, calculation of possible jumps

Plotting fA with given t0 and various values of n shows, that there are two jumps in fA at the position t = t0. The position is independent of n.

The size of the jump can be calculated thus

From below t0

jp = Limit[fA[n, t, t0], t -> t0, Direction -> +1] (* Out[11]= (Sqrt[\[Pi]] Gamma[3/2 + n])/((1 + 2 n) Gamma[1 + n]) *)

and from above t0

jm = Limit[fA[n, t, t0], t -> t0, Direction -> -1] (* Out[12]= -((Sqrt[\[Pi]] Gamma[3/2 + n])/((1 + 2 n) Gamma[1 + n])) *)

The size of one jumps is hence

j = jp - jm (* Out[13]= (2 Sqrt[\[Pi]] Gamma[3/2 + n])/((1 + 2 n) Gamma[1 + n]) *)

The size of the two jumps is therefore twice as large giving

j2 = 2*j (* Out[15]= (4 Sqrt[\[Pi]] Gamma[3/2 + n])/((1 + 2 n) Gamma[1 + n]) *)

Now the antiderivative is equal on both ends of the interval

fA[n, 0, t0] == fA[n, 2 \[Pi], t0] (* Out[17]= True *)

And hence, by the fundamental theorem of calculus, the integral is given by j2.

But this in turn is equal to the expression in the OP

FullSimplify[\[Pi]/2^(2 n - 1) Binomial[2 n, n] == j2] (* Out[21]= True *)

Done.

EDIT #1

Here I'd like to give a more comprehensive anwer to the comment made by sepide, and thanks for this comment.

" @Dr.WolfgangHintze which is true? - sepideh 21 hours ago

1- fundamental theorem of calculus says that the integrand f(x) in Integrate[ f(x), {x,a,b} ] = F(x) should be continuous on the [a,b] interval. 2- fundamental theorem of calculus says that the antiderivative F(x) in Integrate[ f(x), {x,a,b} ] = F(x) should be continuous on the [a,b] interval.

Consider links : 1- Mathematica and the Fundamental Theorem of Calculus 2- Fundamental Theorems of Calculus "

Question 1

My answer is two times no: the theorem does not say this, and furthermore the integrand need not be continuous. This statement is also not contained in reference 1.

Here's a simple example.

A discontinuous function

f[x_] := UnitStep[x - 1/2] Plot[f[x], {x, 0, 1}] (* Output not shown here. *)

It is easily integrated.

fI = Integrate[UnitStep[x - 1/2], {x, 0, 1}] (* Out[30]= 1/2 *)

The antiderivative is

fA[x_] = Integrate[f[x], x] (* Out[28]= (-(1/2) + x) UnitStep[-(1/2) + x] *)

This function is contiuous

Plot[fA[x], {x, 0, 1}] (* Output not shown here *)

Hence the fundamental theorem can be applied, giving for the integral

fA[1] - fA[0] (* Out[31]= 1/2 *)

the expected value, equal to fI.

Question 2

My answer : no, the fundamental theorem of calculus does not say that the antiderivative F(x) in Integrate[ f(x), {x,a,b} ] = F(x) should be continuous on the [a,b] interval.

It says, that it is applicable in its simple form only if the antiderivative is continuous.

I consider the formulation of the first paragraph in ref. 2 an the ref. cited in it unfortunate, to use a polite expression. It should be corrected.

I suggest that "Mister Integrate" Daniel Lichtblau checks it.

I earlier today had a report filed regarding the FTOC wording in MathWorld. The issue is that the antiderivative may need corrections along the integration path in order to be continuous (and this is not stated there). Such corrections are theoretically possible. But only theoretically... — Daniel Lichtblau
– Daniel Lichtblau, Commented Oct 15, 2015 at 18:41

Stack Exchange Network

Find the explicit solution of the integral

2 Answers 2

Linked

Hot Network Questions

Find the explicit solution of the integral

2 Answers 2

Linked

Related

Hot Network Questions