1
$\begingroup$

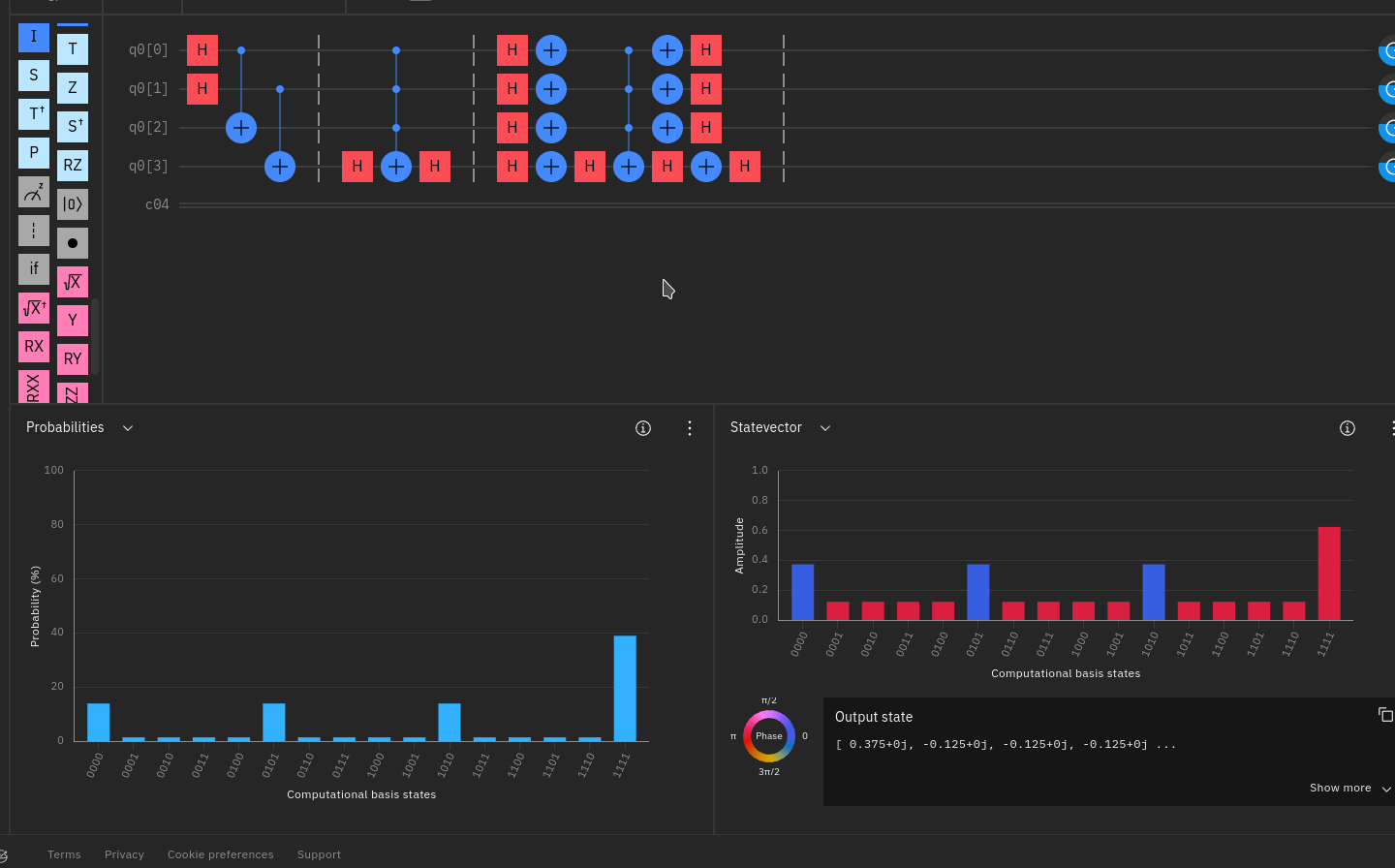
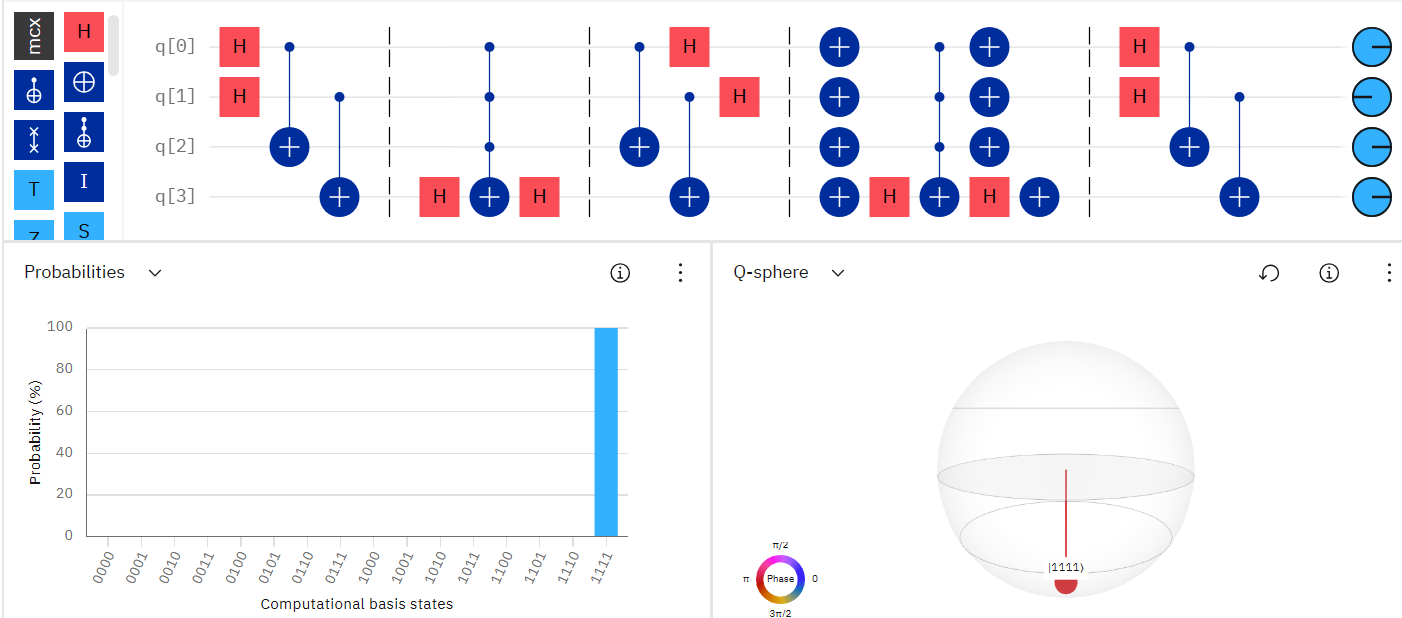
I built a circuit in Qiskit with two GHZ states. In the beginning, I created the superposition $\sim\bigg(|0000\rangle+|0101\rangle+|1010\rangle+|1111\rangle\bigg)$ with two $H$s, and two $CNOT$s.

Now, I want to amplify the result $|1111\rangle$ to over $50\%$. The maximum I got was around $40\%$, and for this case, I calculated that I needed only one iteration. I also tried more, but with no success.

Edit: Can anyone tell me how to implement Amplitude Amplification without needing to apply state initialization operator and the inverse of it because the state initialization operator could be highly complex?

Circuit

Improve this question
$\endgroup$

1 Answer 1

Reset to default
1
$\begingroup$

For Grover algorithm to work, the initial state must be a uniform superposition of all the states. Since your initial state is different, Grover algorithm will not work. Instead, you should use its generalization, Amplitude Amplification.

In amplitude amplification, the Grover operator $\mathcal{Q}$ is $$\mathcal{Q} = \mathcal{A}\mathcal{S_0}\mathcal{A}^\dagger \mathcal{S_f}$$ where $\mathcal{A}$ is the initial state, $\mathcal{S_0}$ is the reflection about all zero state, and $\mathcal{S_f}$ is the oracle. So, you circuit should look like:

enter image description here

Improve this answer
$\endgroup$
1
  • $\begingroup$ Is there a way to implement Amplitude Amplification without having to apply the initial state and the inverse of the initial state, for the case that the state initialization algorithm is highly complex. $\endgroup$ Commented Nov 17, 2023 at 17:26

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.