95

I'm looking for an algorithm that compares two RGB colors and generates a value of their similarity (where similarity means "similar with respect to average human perception").

Any ideas?

EDIT:

Since I cannot answer anymore I decided to put my "solution" as an edit to the question.

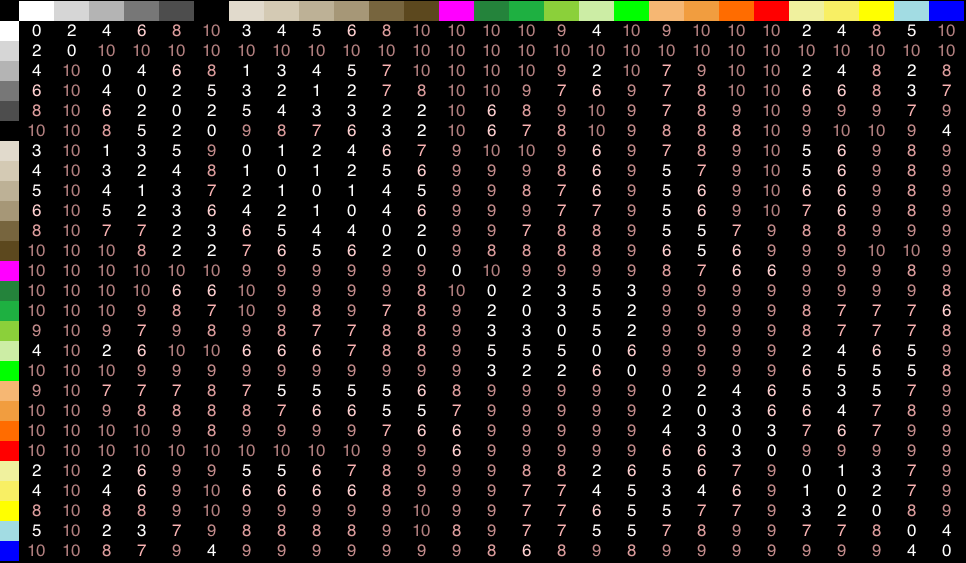
I decided to go with a (very) small subset of true-color in my app, so that I can handle comparison of colors by my own. I work with about 30 colors and use hard-coded distances between them.

Since it was an iPhone app I worked with objective-C and the implementation is more or less a matrix representing the table below, which shows the distances between the colors.

enter image description here

Improve this question
13
  • @Kai: i am trying to implement the same thing. did you go with the YUV approch or did you choose another kind of color space and space distance? Commented Sep 18, 2012 at 14:18
  • 3
    @Thariama I decided to go with a (very) small subset of true-color in my app, so that I can handle comparison of colors by my own. I work with about 50 colors and use hard-coded distances between them. However from all I read and tried and tested when using 2^24 colors YUV did the best job. Commented Sep 18, 2012 at 15:15
  • @Kai: thanks very much for letting me know about your decision and its reasons. that means you are using RGB and create a histogram using 50 colors and speed up your alogithm using predefined distances, correct? what language did you use to implement your algorithm? Commented Sep 19, 2012 at 6:43
  • @Thariama Put it as an edit in the original question. Commented Sep 19, 2012 at 8:45
  • @Kai: thanks very much, too bad there is not a second "+1"-button! Commented Sep 19, 2012 at 9:11

6 Answers 6

Reset to default
62

RGB distance in the euclidean space is not very similar to "average human perception".

You can use YUV color space, it takes into account this factor :

 | Y' | | 0.299 0.587 0.114 | | R | | U | = | -0.14713 -0.28886 0.436 | | G | | V | | 0.615 -0.51499 -0.10001 | | B |

You can also use the CIE color space for this purpose.

EDIT:

I shall mention that YUV color space is an inexpensive approximation that can be computed via simple formulas. But it is not perceptually uniform. Perceptually uniform means that a change of the same amount in a color value should produce a change of about the same visual importance. If you need a more precise and rigourous metric you must definitely consider CIELAB color space or an another perceptually uniform space (even if there are no simple formulas for conversion).

Improve this answer
Sign up to request clarification or add additional context in comments.

7 Comments

Thank you! Can I then go with the euclidian space distance of the Y'UV values?
Sure, but you could also use other distances.
Most probably you want to calculate euclidean distance between UV components only because Y' is the luma component.
Can anyone cite a source for the claim that Euclidean distance in YUV mirrors human perception of differences?
@Bill it doesn't. see the "results" section here: compuphase.com/cmetric.htm
|
27

I would recommend using CIE94 (DeltaE-1994), it's said to be a decent representation of the human color perception. I've used it quite a bit in my computer-vision related applications, and I am rather happy with the result.

It's however rather computational expensive to perform such a comparison:

  1. RGB to XYZ for both colors
  2. XYZ to LAB for both colors
  3. Diff = DeltaE94(LABColor1,LABColor2)

Formulas (pseudocode):

Improve this answer

4 Comments

I preffered this method because of using CIELAB color space, thanks.
XYZ to LAB as in "Hunter-Lab"?
Nevermind... I can see Delta E 1994 uses CIE-L*ab values
What values should be used for WHT-L, WHT-C, WHT-H?
23

There's an excellent write up on the subject of colour distances here: http://www.compuphase.com/cmetric.htm

In case that resource disappears the author's conclusion is that the best low-cost approximation to the distance between two RGB colours can be achieved using this formula (in C code).

typedef struct { unsigned char r, g, b; } RGB; double ColourDistance(RGB e1, RGB e2) { long rmean = ( (long)e1.r + (long)e2.r ) / 2; long r = (long)e1.r - (long)e2.r; long g = (long)e1.g - (long)e2.g; long b = (long)e1.b - (long)e2.b; return sqrt((((512+rmean)*r*r)>>8) + 4*g*g + (((767-rmean)*b*b)>>8)); }
Improve this answer

Comments

16

Human perception is weaker in chroma than intensity.

For example, in commercial video, the YCbCr/YPbPr color spaces (also called Y'UV) reduces the resolution of the chroma info but preserves the luma (Y). In digital video compression such as 4:2:0 and 4:2:2 reduces the chroma bitrate due to relatively weaker perception.

I believe that you can calculate a distance function giving higher priority over luma (Y) and less priority over chroma.

Also, under low intensity, human vision is practically black-and-white. Therefore, the priority function is non-linear in that for low luma (Y) you put less and less weight on chroma.

More scientific formulas: http://en.wikipedia.org/wiki/Color_difference

Improve this answer

Comments

6

Color perception is not Euclidean. Any distance formula will be both good enough and terrible at the same time. Any measure based on Euclidean distance (RGB, HSV, Luv, Lab, ...) will be good enough for similar colors, showing aqua being close to teal. But for non-close values it gets to be arbitrary. For instance, is red closer to green or to blue?

From Charles Poynton's Color FAQ:

The XYZ and RGB systems are far from exhibiting perceptual uniformity. Finding a transformation of XYZ into a reasonably perceptually-uniform space consumed a decade or more at the CIE and in the end no single system could be agreed.

Improve this answer

1 Comment

Thank you. And it's a great, interesting link. For my purpose it's not that important to tell if red is closer to green or blue, but that a light grey is closer to white then a light red and I hope (but not sure yet) that YUV will make it.
-5

Color similarity in the RGB cube is measured by the euclidean distance (use pythagoras formula).

EDIT: On a second thought, this should be true for most other color spaces too.

Improve this answer

3 Comments

No, the Euclidean distance in the RGB space does not correspond to the way the human eye perceives differences between colors. This is the entire reason that color spaces like Lab were created.
no. euclidean distance is one way to measure distance in any cartesian space. it measures distance, not similarity! now you can either pick a different vector space (like cie or yuv) where euclidean distance and similarity sortof coincide, or you use a different measure. but rgb+euclidean don't give satisfiable results.
i thought this too, but then open up a drawing program with a limited number of colors(adobe flash for example, with 216 preset default palette), and put that formula to the test and you get disappointed very very quickly, getting yellows when you clearly need brown, etc.

Start asking to get answers

Find the answer to your question by asking.

Ask question

Explore related questions

See similar questions with these tags.