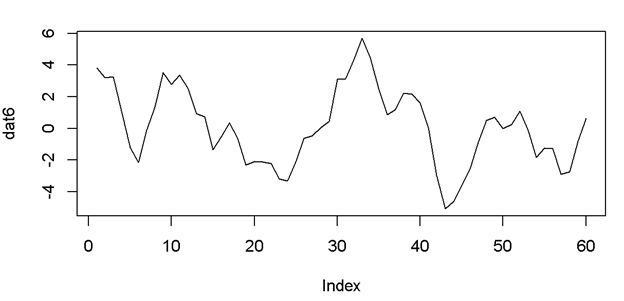
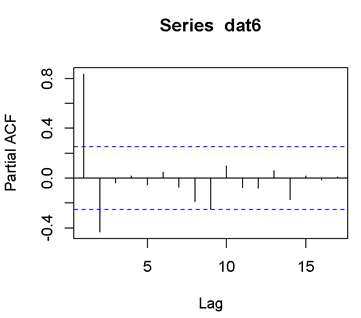
Here is what I obtain when I plot my data set in R. I am now wondering whether this data set is stationary or not. I'm assuming it is stationary since it has no visible trends or seasonality. However, when I look at its ACF, it seems that it's seasonal of cycle length 12. And I would suggest AR(2) model.
Here are the plots of ACF and PACF