A COMPARISON BETWEEN PARALLEL AND SEGMENTATION METHODS USED FOR IMAGE ENCRYPTION-DECRYPTION

A COMPARISON BETWEEN PARALLEL AND SEGMENTATION METHODS USED FOR IMAGE ENCRYPTION-DECRYPTION

• 1.
  International Journal ofComputer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 DOI:10.5121/ijcsit.2016.8509 125 A COMPARISON BETWEEN PARALLEL AND SEGMENTATION METHODS USED FOR IMAGE ENCRYPTION-DECRYPTION Bilal Zahran1 , Ziad Alqadi2 , Jihad Nader3 , Ashraf Abu Ein4 1,2,3,4 Department of Computer Engineering, Al-Balqa Applied University, Jordan ABSTRACT Preserving confidentiality, integrity and authenticity of images is becoming very important. There are so many different encryption techniques to protect images from unauthorized access. Matrix multiplication can be successfully used to encrypt-decrypt digital images. In this paper we made a comparison study between two image encryption techniques based on matrix multiplication namely, segmentation and parallel methods. KEYWORDS Digital image, encryption, decryption, segmentation, parallel processing, speedup, efficiency. 1. INTRODUCTION Digital images are electronic snapshots taken of a scene or scanned from documents, such as photographs, manuscripts, printed texts, and artwork. The digital image is sampled and mapped as a grid of dots or picture elements (pixels). Each pixel is assigned a value (black, white, shades of gray or color), which is represented in binary code (zeros and ones). The binary digits ("bits") for each pixel are stored in a sequence by a computer and often reduced to a mathematical representation (compressed). The bits are then interpreted and read by the computer to produce an analog version for display or printing [1]. Grayscale images can be represented by matrices. Each element of the matrix determines the intensity of the corresponding pixel. For convenience, most of the current digital files use integer numbers between 0 (to indicate black, the color of minimal intensity) and 255 (to indicate white, maximum intensity), giving a total of 256 = 2^8 different levels of gray. Color images, in turn, can be represented by three matrices. Each matrix specifies the amount of Red, Green and Blue that makes up the image. This color system is known as RGB3. The elements of these matrices are integer numbers between 0 and 255, and they determine the intensity of the pixel with respect to the color of the matrix. Thus, in the RGB system, it is possible to represent 2563 = 2^24 = 16777216 different colors [1]. With the rapid growth of computer networks and advances in information technology, a huge amount of digital data is being exchanged over unsecured channels. Major part of transmitted information, either confidential or private, demands for security mechanisms to provide required protection. Therefore, security has become an important issue during the storing and transmission
• 2.
  International Journal ofComputer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 126 of digital data. The security of images is an application layer technology to guard the transmitted information against unwanted disclosure as well as to protect the data from modification while in transit. It includes several aspects like copyright protection, authentication, confidentiality and access control. It is argued that traditional encryption algorithms are not preferable for image encryption for two reasons. One is that the image size is always more than text size. Therefore, traditional cryptosystems take longer time to encrypt the image data. The other is that the size of decrypted text must be equal to the original text size. However, this requirement is not necessary for image data. Due to the characteristic of human perception, a small distortion in decrypted image is usually acceptable. Three different ways to protect digital data from unauthorized eavesdropping are cryptography, steganography and watermarking. Among these three techniques, cryptography has become one of the major tools to provide high level of security. Cryptography deals with the development of techniques for converting information between intelligible and unintelligible forms. It deals with the content confidentiality and access control. In secure communications using cryptography, which is the main focus of the present work, the encryption and decryption operations are guided by one or more keys. Techniques that use same secret key for encryption and decryption are grouped under private key cryptography. Alternately, encryption and decryption keys are different or computationally it may not be feasible to derive one key even though the knowledge of other key, such cryptographic methods are known as public key cryptography. The present work focuses on the development of private key image cryptographic algorithm for providing high level of security [2]. Many techniques and methods were proposed for digital image encryption-decryption [3, 4, and 5], but all these methods and techniques suffer from the security level and the big time needed to impalement encryption and decryption. 2. LITERATURE REVIEW Many studies that compare image encryption techniques were conducted: In [6] Comparative analysis of Advanced Encryption Standard, Compression Friendly Encryption Scheme, Chaotically Coupled Chaotic Map Encryption Scheme and a Bernoulli Map Based Encryption Scheme are done. In [7] the researchers did a literature review on existing work which was done form different techniques for image encryption and also gave the general introduction about images and image encryption with advantages and disadvantages. In [8] the researchers presented a survey of over 25 research papers dealing with image encryption techniques scrambled the pixels of the image and decrease the correlation among the pixels. In [9] the researchers classified various image encryption schemes and analyzed them with respect to various parameters like tunability, visual degradation, compression friendliness, format compliance, encryption ratio, speed, and cryptographic security. In [10] the researchers analyzed and compared current image encryption algorithms namely, Mirror-like image encryption and Visual Cryptography.
• 3.
  International Journal ofComputer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 127 3. PARALLEL ENCRYPTION-DECRYPTION FOR IMAGE The OpenMP library is an API (Application Programming Interface) for writing shared memory parallel applications in programming languages such as matlab, C++. This API consists of compiler directives, runtime routines, and Environmental variables. Some the advantages of OpenMP includes: good performance, portable (it is supported by a large number of compilers), requires very little programming effort and allows the program to be parallelized incrementally. OpenMP is widely available and used, mature, lightweight, and ideally suited for multi-core architectures. Data can be shared or private in the OpenMP memory model. When data is private it is visible to one thread only, when data is public it is global and visible to all threads. OpenMP divides tasks into threads; a thread is the smallest unit of a processing that can be scheduled by an operating system. The master thread assigns tasks unto worker threads. Afterwards, they execute the task in parallel using the multiple cores of a processor [11]. Multiplication of large matrices requires a lot of computation time as its complexity is O(n ^3 ), where n is the dimension of the matrix. Because most current applications require higher computational throughputs, many algorithms based on sequential and parallel approaches were developed to improve the performance of matrix multiplication. Even with such improvements [12], [13], for example, Stassen's algorithm for sequential matrix multiplication [13] has shown a limitation in performance. For this reason, parallel approaches have been examined for decades. Most of parallel matrix multiplication algorithms use matrix decomposition that is based on the number of processors available. This includes [14],[15]: the systolic algorithm, Cannon's algorithm, Fox and Otto's algorithm, PUMMA (Parallel Universal Matrix Multiplication), SUMMA (Scalable Universal Matrix Multiplication) and DIMMA (Distribution Independent Matrix Multiplication). Each one of these algorithms uses the matrices that decomposed into sub- matrices. During execution process, a processor calculates a partial result using the sub-matrices that are currently accessed by it. It successively performs the same calculation on new sub matrices, adding the new results to the previous [12], [13]. Parallel processing for matrix multiplication is an efficient method of multiplication, but as shown in [16] the speedup of multiplication is limited to the available number of existing processors. 4. IMPLEMENTATION 4.1 PARALLEL METHOD IMPLEMENTATION Contemporary desktop and laptop PCs are, more often than not, equipped with multi-core processors. On the one hand, the MATLAB Parallel Computing Toolbox may be used to help speed up computations on these PCs. On the other hand, because these cores, or threads, share a common memory, many of MATLAB’s thread-parallel enabled functions may readily be put to work autonomously without any coding modifications. This is referred to as implicit parallelism to distinguish it from explicit parallelism for which the PCT belongs. Vector operation is the necessary, but not sufficient, trigger for implicit parallel computation. The particular application or algorithm, and the amount of computations also help MATLAB to determine whether an application will be performed with multithreads. A digital image was represented by a matrix and the encryption phase was implemented by applying the following steps:
• 4.
  International Journal ofComputer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 128 • Get the original image matrix. • Generate a random matrix to be used as a private key for encryption. • Apply matrix multiplication of the original matrix and the key to get the encrypted image. • The decryption phase can be implemented applying the following steps: • Get the encrypted image. • Use the private key. • Apply matrix multiplication of the encrypted image with the inverse of the private key to get the decrypted (original image). Table 1 shows the parallel implementation results Table 1. Parallel processing implementation results No. of threads Encryption- decryption time (in secs) * Speedup † Efficiency(%) ‡ 1 1.9672 1 100 2 1.0990 1.79 89.5000 4 0.6346 3.1 77.5000 8 0.4015 4.9 61.2500 * Timings collected on Intel Xeon i7 2.93 GHz processors. † Speedup = T1/TN; where T1 and TN are the wall clock time for 1 and N threads, respectively. ‡ Efficiency = 100*Speedup/N 4.2 SEGMENTATION METHOD IMPLEMENTATION The encryption phase can be implemented applying the following steps: 1) Get the original image matrix. 2) If the matrix is not square reshape it to square by padding zeros. 3) Select the number of segment to be used to segment the original matrix. 4) Divide the image into equal sizes segments. 5) For each segment generate a square matrix with size equal segment size to be used as a private key for encryption-decryption. 6) Encrypt each segment by applying matrix multiplication. 7) Reshape the encrypted matrix to the original size. The decryption phase can be implemented applying the following steps: 1) Get the encrypted image matrix. 2) If the matrix is not square reshape it to square by padding zeros. 3) Use the number of segment to be used to segment the original matrix. 4) Divide the image into equal sizes segments. 5) For each segment use its a private key. 6) Decrypt each segment by applying matrix multiplication using the inverse of the private key. 7) Reshape the decrypted matrix to the original size to get the original image.
• 5.
  International Journal ofComputer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 129 This method was implemented using matlab code and table 2 shows some experimental results: For comparisons the same image with size 2000*2000 was encrypted-decrypted using segmentation method and the results are shown in table 3. Table 2. Segmentation Method Encrypting-decrypting Image (size 4096*4096) No. of segments Segment size #of private keys Encryption time(s) Decryption time(s) Total time(s) Speedup 1 4096*4096 1 28.829000 61.371000 90.2000 1 2 2048*2048 2 3.666000 7.924000 23.1800 3.8913 4 1024*1024 4 0.468000 1.061000 6.1160 14.7482 8 512*512 8 0.063000 0.156000 1.7520 51.4840 16 256*256 16 0.015000 0.016000 0.4960 181.8548 32 128*128 32 0.000300 0.000300 0.0192 4697.9 Table 3. Segmentation Method Encrypting-decrypting Image (size 2000*2000) No. of segments Encryption- decryption time (in secs) * Speedup † Efficiency (%)‡ 1 1.9672 1 100 2 0.5595 3.5160 351.6 4 0.2013 9.7724 977.24 8 0.1318 14.9255 1492.55 5. DISCUSSION OF RESULTS From tables 1, 2 and 3 we can compare the processing time and find the speedup of segmentation method over parallel processing method, the results of comparisons are shown in table 4. Table 4. Comparisons Results No. of threads/segments Encryption- decryption time using parallel processing(Sec) Encryption- decryption time using segmentation(Sec) Speedup 1 1.9672 1.9672 1 2 1.0990 0.5595 1.9643 4 0.6346 0.2013 3.1525 8 0.4015 0.1318 3.0463 From table 4 we can see that using segmentation method is more efficient to encrypt-decrypt the image and as illustrated in figures 1 and 2.
• 6.
  International Journal ofComputer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 130 Figure 1. Speedup Figure 2. Encryption-DecryptionTime 6. CONCLUSION Matrix multiplication can be successfully used to encrypt-decrypt digital images. Two methods of matrix multiplication were compared and from the obtained results we can conclude that segmentation method provides a high secure method of encryption-decryption by using a set of 1 2 3 4 5 6 7 8 0 5 10 15 #of threads/segments Speedup Speedup) Parallel Segmentation 1 2 3 4 5 6 7 8 0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 #of threads/segments Enc-Dectime(s) Encryption-decryption time(s) Parallel Segmentation
• 7.
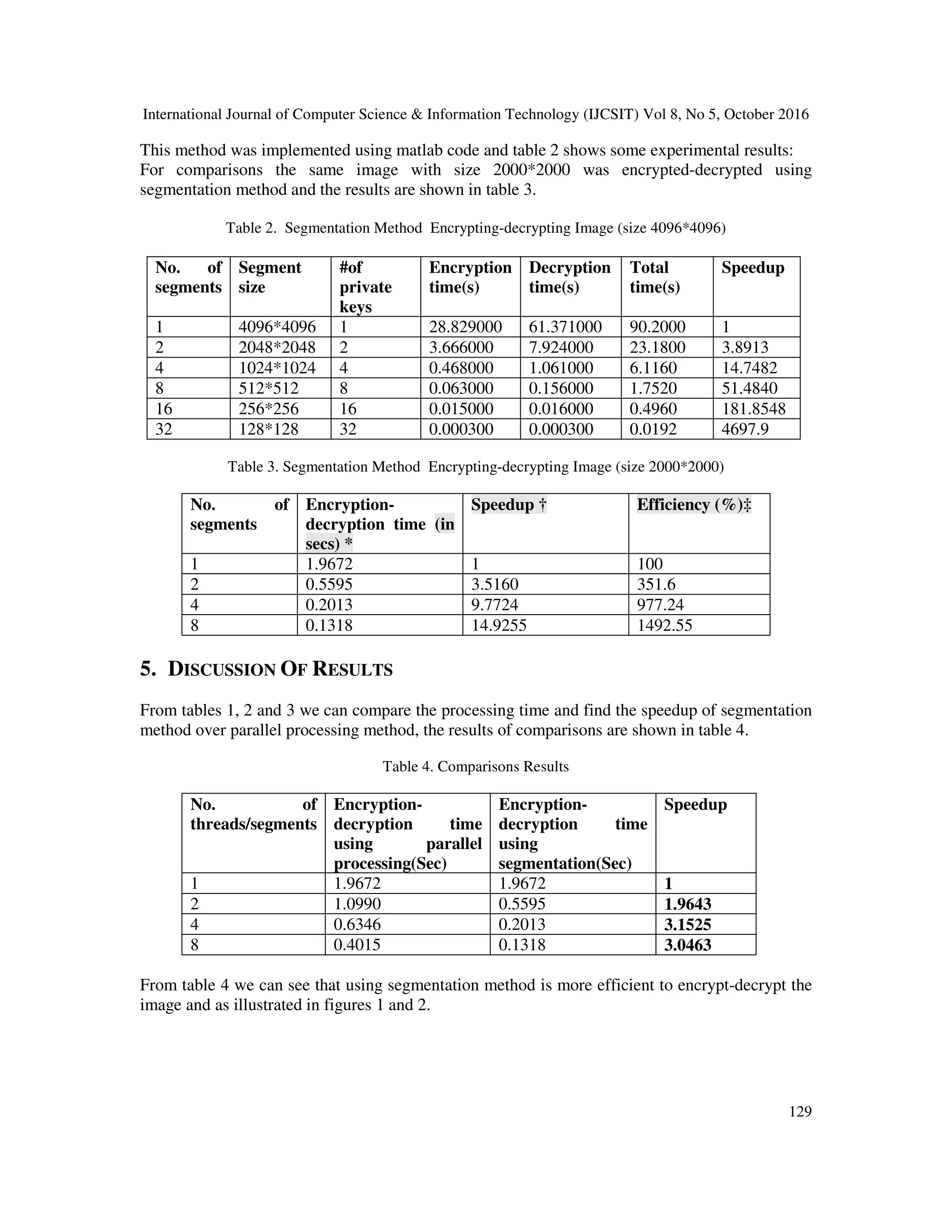
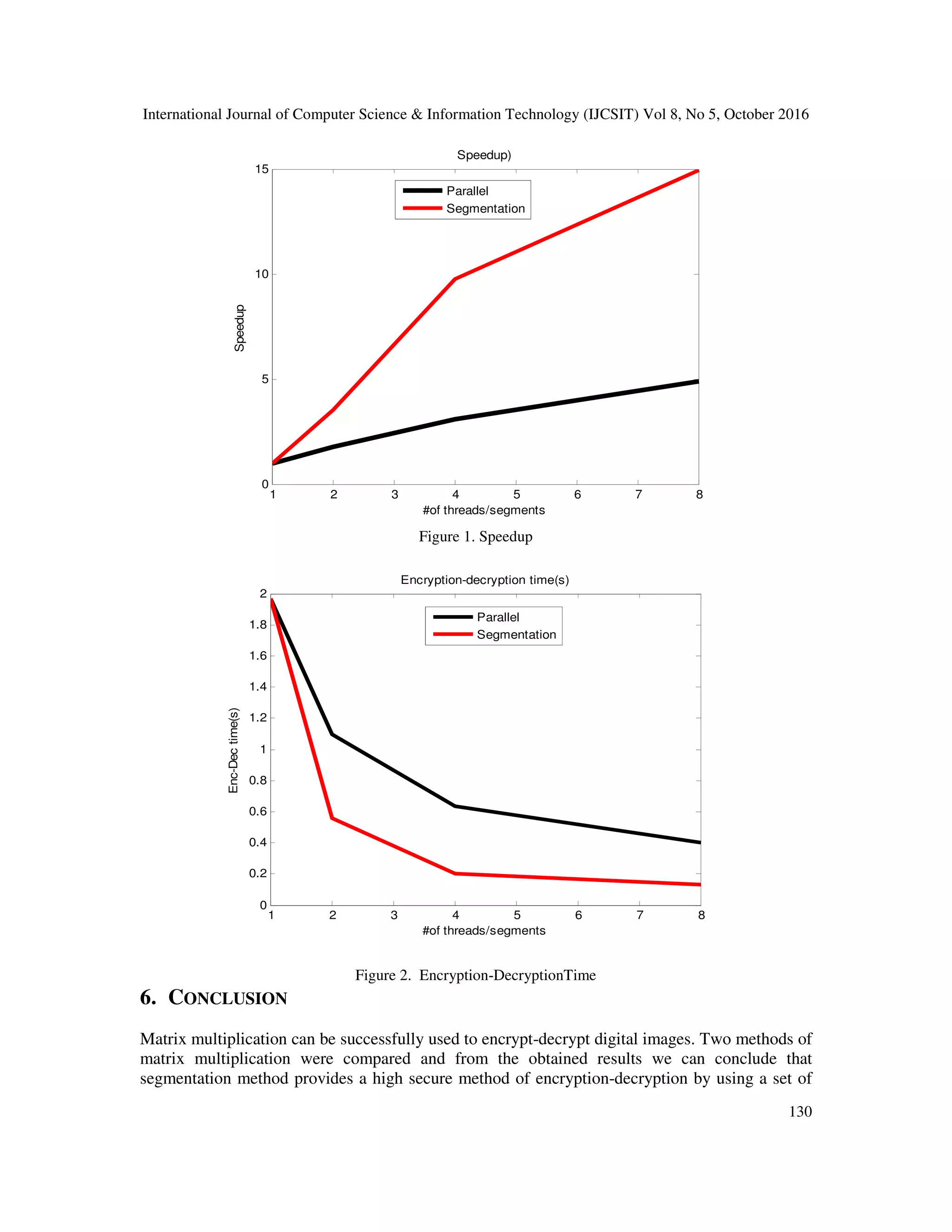
  International Journal ofComputer Science & Information Technology (IJCSIT) Vol 8, No 5, October 2016 131 private random keys. Furthermore, the efficiency of using segmentation method is higher than any other method even comparing with parallel computation method. REFERENCES [1] R. Gonzalez, R. Woods (2008). Digital Image Processing, 3rd Edition. Pearson Prentice Hall. ISBN 978-0-13-168728-8. [2] K. Narendra (2012), "Design and Analysis of A Novel Digital Image Encryption Scheme", International Journal of Network Security & Its Applications (IJNSA), Vol.4, No.2. [3] T. Sivakumar , and R.Venkatesan (2013), "A Novel Image Encryption Approach using Matrix Reordering" , WSEAS TRANSACTIONS on COMPUTERS, Issue 11, Volume 12, pp 407-418. [4] H. Gao, Y. Zhang, S. Liang and D. Li,( 2006) “A New Chaotic Algorithm for Image Encryption”, Elsevier Science Direct, vol. 29, no. 2, pp.393-399. [5] K. Loukhaoukha, J. Chouinard, and A. Berdai, (2011 ) “A Secure Image Encryption Algorithm Based on Rubik's Cube Principle”, Journal of Electrical and Computer Engineering, , pp. pp.1-13. [6] J. Ahmad, S. Oun Hwang and A. Ali (2015), " An Experimental Comparison of Chaotic and Non- chaotic Image Encryption Schemes", Wireless personal communication, Volume 84, Issue 2, pp 901– 918. [7] R. Yadavi, M. Beg2 & M. Tripathi (2013), "Image Encryption Techniques: A Critical Comparison", International Journal of Computer Science Engineering and Information Technology Research (IJCSEITR) ISSN 2249-6831 Vol. 3, Issue 1. [8] R. Pakshwar, V. Kumar Trivedi and V. Richhariya (2013), "A Survey On Different Image Encryption and Decryption Techniques, (IJCSIT) International Journal of Computer Science and Information Technologies, Vol. 4 (1) , 2013, 113 – 116. [9] J. Shah and V. Saxena (2011), "Performance Study on Image Encryption Schemes", IJCSI International Journal of Computer Science Issues, Vol. 8, Issue 4, No 1. [10] I. Öztürk and I.Sogukpınar (2007), "Analysis and Comparison of Image Encryption Algorithms", International Journal of Computer, Electrical, Automation, Control and Information Engineering Vol:1, No:3. [11] R. Chowdhury, "Parallel Computing with OpenMP to solve matrix Multiplication", UCONN BIOGRID REU Summer 2010 ,Department of Computer Science & Engineering University of Connecticut, Storrs, CT 06269. [12] Z.A. Alqadi, M. Aqel, I.M. El Emary, (2008) "Performance Analysis and Evaluation of Parallel Matrix Multiplication Algorithms" , World Applied Sciences Journal, vol. 5 (2):, ISSN 1818-4952. [13] Z.A. Alqadi, A. Abu-Jazzar (2005), Analysis Of Program Methods Used For Optimizing Matrix Multiplication, Journal of Engineering, vol. 15 n. 1, pp. 73-78. [14] R.C. Agarwal, F.G. Gustavson and M. Zuibar, (1994), A high performance matrix multiplication algorithm on a distributed memory parallel computer using overlapped communication, IBM J. Res. Develop., Volume 38, Number 6. [15] Agarwal, R.C., S.M. Balle, F.G. Gustavson, M. Joshi and P. Palkar, (1995). A 3-Dimensional Approach to Parallel Matrix Multiplication, IBM J. Res.Develop., Volume 39, Number 5, pp: 1-8, Sept. [16] H. Alasha'ary, K. Matrouk, A. Al-Hasanat, Z. Alqadi, H. Al-Shalabi (2013), Improving Matrix Multiplication Using Parallel Computing, International Journal on Information Technology (I.RE.I.T.) Vol. 1, N. 6 ISSN 2281-2911.